Theorem Pythagoras

Mewn mathemateg, Theorem Pythagoras yw'r berthynas rhwng tair ochr triongl ongl sgwâr. Enwir y theorem ar ôl y mathemategwr Pythagoras o wlad Groeg. Tadogir darganfod a phrofi'r theorem ar Pythagoras, ond mewn gwirionedd yr oedd y theorem yn hysbys cyn cyfnod Pythagoras.
Dyma'r theorem fel y'i fynegir yn gyffredinol:
Mewn unrhyw driongl ongl sgwâr, mae arwynebedd y sgwâr sydd ag ochr yr hypotenws, yn hafal i swm arwynebau y sgwariau a'u hochrau eraill (sydd yn cwrdd ar yr ongl sgwâr).
Os taw c yw hyd yr hypotenws, ac a a b yw hydoedd y ddwy ochr arall, gellir mynegi'r hafaliad fel y ganlyn:
neu er mwyn datrys c:
Ar gyfer triongl sydd yn driongl ongl sgwâr, rhydd yr hafaliad hwn berthynas syml rhwng y tair ochr, fel y gellid darganfod hyd unrhyw ochr o wybod hyd y ddwy ochr arall.
Profwyd y ddamcaniaeth (theorem) sawl gwaith trwy lawer o wahanol ddulliau - y nifer mwyaf o weithiau, o bosibl ar gyfer unrhyw theorem fathemategol. Mae'r profion mathemategol yn amrywiol, gan gynnwys proflenni geometrig a phroflenni algebraidd, gyda rhai yn dyddio'n ôl filoedd o flynyddoedd.
Gellir cyffredinoli'r theorem mewn amrywiol ffyrdd: i ofodau dimensiwn uwch, i fannau nad ydynt yn Ewclidaidd, i wrthrychau nad ydynt yn drionglau cywir, ac i wrthrychau nad ydynt yn drionglau o gwbl ond yn solidau n-dimensiwn. Mae theorem Pythagoras wedi denu diddordeb y tu allan i fathemateg fel symbol o fathemateg astrus, cyfrinachedd, neu bŵer deallusol; mae cyfeiriadau poblogaidd mewn llenyddiaeth: mae dramâu, sioeau cerdd, caneuon, stampiau a chartwnau yn ddirifedi, rif y gwlith.
Enghreifftiau gyda chyfanrifau
[golygu | golygu cod]Er nad oes hydoedd cyfanrifol gan ochrau'r mwyafrif o drionglau ongl sgwâr, mae gan nifer o drionglau hydoedd hollol gyfanrifol, gan gynnwys yr enghreifftiau enwog ac . Yn gyffredinol, ar gyfer unrhyw rif , mae triongl ongl sgwâr yn bodoli gyda hydoedd . Trwy ddewis bod yn gyfanrif, mae'n hawdd dod o hyd i drionglau â hydoedd cyfanrifol (cynhyrcha ac yr enghreifftiau uchod). Fel soniwyd mae'r ffwythiant hwn yn cynhyrchu trionglau ongl sgwâr gyda yn unig, ond mae trionglau ongl sgwâr a hydoedd cyfanrifol eraill i gael; e.e. .
Prawf aildrefnu
[golygu | golygu cod]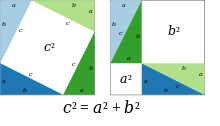
Mae'r ddau sgwâr mawr a ddangosir yn y ffigur yn cynnwys pedwar triongl sydd yn union yr un fath, a'r unig wahaniaeth rhwng y ddau sgwâr mawr yw bod y trionglau wedi'u trefnu'n wahanol. Felly, mae'n rhaid fod gan y gofod gwyn ym mhob un o'r ddau sgwâr mawr arwynebedd cyfartal. Mae cyfateb arwynebedd y gofod gwyn hwn yn cynhyrchu theorem Pythagorean,QED[1]
Mae Heath yn rhoi’r prawf hwn yn ei sylwebaeth ar Gynigiad I.47 yn Elfennau Euclid, ac yn sôn am gynigion Bretschneider a Hankel y gallai Pythagoras fod wedi gwybod y prawf hwn. Mae Heath ei hun yn ffafrio cynnig gwahanol ar gyfer prawf Pythagoras, ond mae'n cydnabod o ddechrau ei drafodaeth "nad yw'r llenyddiaeth Roegaidd sydd gennym yn perthyn i'r pum canrif gyntaf ar ôl Pythagoras yn cynnwys unrhyw ddatganiad sy'n nodi hyn nac unrhyw ddarganfyddiad geometrig mawr penodol arall iddo."[2] Mae ysgolheictod diweddar wedi bwrw amheuaeth gynyddol ar unrhyw fath o rôl i Pythagoras fel crëwr gwaith mathemategol, er bod y ddadl am hyn yn parhau.
Ffurfiau eraill o'r theorem
[golygu | golygu cod]Os yw c yn dynodi hyd yr hypotenws ac mae a a b yn dynodi hyd y ddwy ochr arall, gellir mynegi theorem Pythagoras fel hafaliad Pythagoras:
Os yw hyd a a hyd b yn hysbys, yna gellir cyfrifo c fel
Os yw hyd y hypotenws c ac un ochr ( a neu b ) yn hysbys, yna gellir cyfrifo hyd yr ochr arall fel
Mae hafaliad Pythagoras yn cysylltu ochrau triongl ongl sgwâr mewn ffordd syml: os yw hyd unrhyw ddwy ochr yn hysbys gellir dod o hyd i hyd i'r drydedd ochr. Canlyniad arall y theorem yw bod yr hypotenws mewn unrhyw driongl dde yn fwy nag unrhyw un o'r ochrau eraill, ond yn llai na'u cyfanswm.
Un cyffredinoliad o'r theorem hon yw deddf cosin, sy'n caniatáu cyfrifo hyd unrhyw ochr i unrhyw driongl, os yw'r ddwy ochr arall a'r ongl rhyngddynt yn wybyddus. Os yw'r ongl rhwng yr ochrau eraill yn ongl sgwâr, mae cyfraith cosin yn lleihau i'r hafaliad Pythagoras.
Proflenni eraill o'r theorem
[golygu | golygu cod]Efallai bod gan y theorem hon mwy o brofion ng unrhyw theorem arall; mae'r llyfr The Pythagorean Proposition yn cynnwys 370 prawf.[3]
Prawf gan ddefnyddio trionglau tebyg
[golygu | golygu cod]
Mae'r prawf hwn yn seiliedig ar gymesuredd ochrau dwy driongl tebyg, hynny yw, yn seiliedig ar y ffaith bod cymhareb unrhyw ddwy ochr gyfatebol o drionglau tebyg yr un fath waeth beth yw maint y trionglau.
Gadewch i ABC gynrychioli triongl dde, gyda'r ongl sgwâr wedi'i leoli yn C, fel y dangosir yn y diagram. Tynnwch yr uchder o bwynt C, a galwch H ei groestoriad â'r ochr AB. Mae pwynt H yn rhannu hyd yr hypotenws c yn rhannau d ac e. Mae'r triongl newydd ACH yn debyg i driongl ABC, oherwydd mae gan y ddau ongl sgwâr (trwy ddiffiniad o'r uchder), ac maen nhw'n rhannu'r ongl yn A, sy'n golygu y bydd y drydedd ongl yr un peth yn y ddwy driongl hefyd, wedi'i marcio â θ yn y ffigur. Trwy ymresymiad tebyg, mae'r triongl CBH hefyd yn debyg i ABC. Mae prawf tebygrwydd y trionglau yn gofyn bod y triongl yn cynosod: mae swm yr onglau mewn triongl yn ddwy ongl sgwâr, ac mae'n cyfateb i'r cynosodiad cyfochrog. Mae tebygrwydd y trionglau yn arwain at gydraddoldeb cymarebau ochrau cyfatebol:
gyda'r canlyniad cyntaf yn cyfateb i gosbin yr onglau θ, ond mae'r ail ganlyniad yn cyfateb i'w sinau .
Gellir ysgrifennu'r cymarebau hyn fel
Mae crynhoi'r ddau gydraddoldeb hyn yn arwain at
sydd, ar ôl ei symleiddio, yn mynegi theorem Pythagoras:
Mae rôl y prawf hwn mewn hanes yn destun llawer o ddyfalu. Y cwestiwn sylfaenol yw pam na ddefnyddiodd Euclid y prawf hwn, ond yn hytrach, dyfeisiodd un arall. Un rhagdybiaeth yw bod y prawf gan drionglau tebyg yn cynnwys theori cyfrannau, pwnc na thrafodwyd tan yn ddiweddarach yn yr Elfennau, a bod angen datblygu theori cyfrannau ymhellach bryd hynny.[4][5]
Prawf Euclid
[golygu | golygu cod]
Yn fras, dyma'r prawf yn yr Elfennau gan Euclid: rhennir y sgwâr mawr yn betryal chwith a dde. Mae triongl wedi'i lunio sydd â hanner arwynebedd y petryal chwith. Yna mae triongl arall yn cael ei lunio sydd â hanner arwynebedd y sgwâr ar yr ochr chwith-bellaf. Dangosir bod y ddwy driongl hyn yn gyfath, gan brofi bod gan y sgwâr hwn yr un arwynebedd â'r petryal ar y chwith. Dilynir y ddadl hon gan fersiwn debyg ar gyfer y petryal dde a'r sgwâr sy'n weddill. Gan roi'r ddau betryal at ei gilydd i ddiwygio'r sgwâr ar yr hypotenws, mae ei arwynebedd yr un fath â swm arwynebedd y ddau sgwâr arall. Mae'r manylion yn dilyn.
Gadewch i A, B, C fod yn fertigau triongl sgwâr, gyda'r ongl sgwâr yn A. Gollyngir perpendicwlar o A i'r ochr gyferbyn â'r hypotenws yn y sgwâr ar yr hypotenws. Mae'r llinell honno'n rhannu'r sgwâr ar yr hypotenws yn ddau betryal, pob un â'r un arwynebedd ag un o'r ddau sgwâr ar y coesau.
I gael y prawf ffurfiol, mae angen pedwar lemmata elfennol arnom:
- Os oes dwy ochr i'r ddau driongl o'r un sy'n hafal i ddwy ochr y llall, pob un i bob un, a'r onglau a gynhwysir gan yr ochrau hynny yn gyfartal, yna mae'r trionglau yn gyfath (ochr-ongl-ochr).
- Mae arwynebedd triongl yn hanner arwynebedd unrhyw baralelogram ar yr un sylfaen ac sydd â'r un uchder.
- Mae arwynebedd petryal yn hafal i luoswm dwy ochr gyfagos.
- Mae arwynebedd sgwâr yn hafal i luoswm dwy o'i ochrau (yn dilyn o 3).
Nesaf, mae pob sgwâr uchaf yn gysylltiedig â thriongl sy'n gyfath â thriongl arall ac sy'n perthyn, yn ei dro ag un o ddau betryal sy'n ffurfio'r sgwâr isaf.

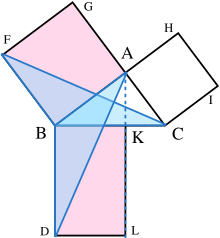
Mae'r prawf fel a ganlyn:
- Gadewch i ACB fod yn driongl ongl sgwâr gyda CAB yn ongl sgwâr.
- Ar bob un o'r ochrau BC, AB, ac CA, tynnir sgwariau, CBDE, BAGF, ac ACIH, yn y drefn honno. Mae llunio sgwariau yn gofyn am y theoremau sy'n union o flaen theoremau Euclid, ac mae'n dibynnu ar y cynosodiad cyfochrog.[6]
- O A, tynnwch linell yn gyfochrog â BD a CE. Bydd yn croestorri BC a DE yn K a L, yn y drefn honno.
- Ymunwch â CF ac AD, i ffurfio'r trionglau BCF a BDA.
- Mae onglau CAB a BAG ill dau yn onglau sgwâr; felly mae C, A, a G yn gyfochrog.
- Mae onglau CBD a FBA ill dau yn onglau sgwâr; felly mae ongl ABD yn hafal i ongl FBC, gan fod y ddau yn gyfanswm ongl sgwâr ac ongl ABC.
- Gan fod AB yn hafal i FB, mae BD yn hafal i BC ac mae ongl ABD yn hafal i ongl FBC, rhaid i driongl ABD felly fod yn gyfath â thriongl FBC.
- Gan fod A-K-L yn llinell syth, yn gyfochrog â BD, yna mae gan betryal BDLK ddwywaith arwynebedd triongl ABD oherwydd eu bod yn rhannu'r sylfaen BD ac mae ganddynt yr un uchder BK, hy, llinell sy'n normal i'w sylfaen gyffredin, gan gysylltu'r llinellau cyfochrog BD ac AL. (lemma 2)
- Gan fod C yn cyd-fynd ag (collinear with) A a G, a bod y llinell hon yn gyfochrog ag FB, yna mae'n rhaid i'r sgwâr BAGF fod ddwywaith mewn arwynebedd i driongl FBC.
- Felly, rhaid i betryal BDLK fod â'r un arwynebedd â sgwâr BAGF = AB2.
- Trwy gymhwyso camau 3 i 10 i ochr arall y ffigur, gellir dangos yn yr un modd bod yn rhaid i betryal CKLE fod â'r un ardal â sgwâr ACIH = AC2.
- Gan ychwanegu'r ddau ganlyniad hyn, AB2 + AC2 = BD × BK + KL × KC
- Gan fod BD = KL, BD × BK + KL × KC = BD(BK + KC) = BD × BC
- Felly mae AB2 + AC2 = BC2, gan fod CBDE yn sgwâr.
Y prawf hwn (sy'n ymddangos yn Elfennau Euclid fel Cynnig 47 yn Llyfr Mae 1,[7]) sy'n dangos mai arwynebedd y sgwâr ar y hypotenws yw swm arwynebedd y ddau sgwâr arall.[8] Mae hyn yn hollol wahanol i'r prawf yn ôl tebygrwydd trionglau, y tybir ei fod yn brawf a ddefnyddiodd Pythagoras.[5][9]
Profi trwy ddyraniad ac aildrefnu
[golygu | golygu cod]Trafodwyd uchod prawf Pythagoras, sy'n brawf trwy aildrefnu. Mae'r un syniad yn cael ei gyfleu gan yr animeiddiad ar y chwith isod, sy'n cynnwys sgwâr mawr, ochr a + b, sy'n cynnwys pedwar triongl sgwârtriongl ongl sgwâr sy'n union yr un fath. Dangosir y trionglau mewn dau drefniant, ac mae'r cyntaf yn gadael dau sgwâr a2 a b2 heb eu gorchuddio, a'r ail ohonynt yn gadael sgwâr c2 heb ei orchuddio. Mae'r arwynebedd sy'n cael ei gwmpasu gan y sgwâr allanol byth yn newid, ac arwynebedd y pedwar trionglau yr un fath ar y dechrau ac ar y diwedd, felly mae'n rhaid i'r arwynebedd y sgwariau du fod yn gyfartal, a2 + b2 = c2.
Rhoddir ail brawf trwy aildrefnu gan yr animeiddiad canol. Mae sgwâr mawr yn cael ei ffurfio gydag arwynebedd c2, o bedair triongl sgwâr union yr un fath, gydag ochrau a, b ac c, wedi'u gosod o amgylch sgwâr canolog bach. Yna mae dau betryal yn cael eu ffurfio gydag ochrau a a b trwy symud y trionglau. Mae cyfuno'r sgwâr llai â'r petryalau hyn yn cynhyrchu dau sgwâr o ardaloedd a2 a b2, ac y mae'n rhaid iddynt fod â'r un arwynebedd â'r sgwâr mawr cychwynnol.[10]
Mae'r drydedd ddelwedd ar y dde hefyd yn rhoi prawf. Rhennir y ddau sgwâr uchaf fel y dangosir gan y cysgod glas a gwyrdd, yn ddarnau y gellir eu haildrefnu i ffitio yn y sgwâr isaf ar y hypotenws - neu i'r gwrthwyneb gellir rhannu'r sgwâr mawr fel y dangosir yn ddarnau sy'n llenwi'r ddau arall. Yr enw ar y ffordd hon o dorri un ffigur yn ddarnau a'u haildrefnu i gael ffigur arall yw dyraniad (dissection). Mae hyn yn dangos bod arwynebedd y sgwâr mawr yn hafal i arwynebedd y ddau lai.[11]
 |
 |
 |
Prawf Einstein trwy ddadraniad heb aildrefnu
[golygu | golygu cod]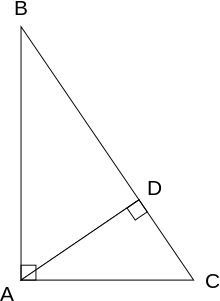
Rhoddodd Albert Einstein brawf trwy ddadraniad lle nad oes angen symud y darnau.[12] Yn lle defnyddio sgwâr ar yr hypotenws a dau sgwâr ar y coesau, gellir defnyddio unrhyw siâp arall sy'n cynnwys yr hypotenws, a dau siâp tebyg gyda phob un yn cynnwys un o ddwy goes yn lle'r hypotenws. Ym mhrawf Einstein, y siâp sy'n cynnwys yr hypotenws yw'r triongl sgwâr ei hun. Mae'r dyraniad yn cynnwys gollwng perpendicwlar o fertig ongl sgwâr y triongl i'r hypotenws, a thrwy hynny rannu'r triongl cyfan yn ddwy ran. Mae gan y ddwy ran hynny yr un siâp â'r triongl dde gwreiddiol, ac mae ganddyn nhw goesau'r triongl gwreiddiol â'u hypotenysau, a swm eu hardaloedd yw'r triongl gwreiddiol. Oherwydd bod cymhareb arwynebedd triongl sgwâr â sgwâr ei hypotenws yr un peth ar gyfer trionglau tebyg, mae'r berthynas rhwng arwynebedd y tair triongl yn dal ar gyfer sgwariau ochrau'r triongl mawr hefyd.
Profion algebraidd
[golygu | golygu cod]
Gellir profi'r theorem yn algebraig trwy ddefnyddio pedwar copi o driongl sgwâr gydag ochrau a, b ac c, wedi'u trefnu y tu mewn i sgwâr ag ochr c fel yn hanner uchaf y diagram.[13] Mae'r trionglau yn debyg i arwynebedd , tra bod gan y sgwâr bach ochr b − a ac arwynebedd (b − a)2. Mae arwynebedd y sgwâr mawr felly yn
Ond sgwâr yw hwn gydag ochr c ac arwynebedd c2, felly
Mae prawf tebyg yn defnyddio pedwar copi o'r un triongl wedi'u trefnu'n gymesur o amgylch sgwâr ag ochr c, fel y dangosir yn rhan isaf y diagram.[14] Mae hyn yn arwain at sgwâr mwy, gydag ochr a + b ac arwynebedd (a + b)2 . Rhaid i'r pedair triongl a'r ochr sgwâr c fod â'r un arwyneb â'r sgwâr mwy,
sy'n rhoi

Cyhoeddwyd prawf cysylltiedig gan Arlywydd yr UD James A. Garfield (a oedd yn Gynrychiolydd yr Unol Daleithiau ar y pryd) - gweler y diagram.[15][16] Yn lle sgwâr mae'n defnyddio trapesoid, y gellir ei adeiladu o'r sgwâr yn yr ail o'r profion uchod trwy rannu ar hyd croeslin y sgwâr mewnol, i roi'r trapesoid fel y dangosir yn y diagram. Gellir cyfrifo bod arwynebedd y trapesoid yn hanner arwynebedd y sgwâr, hynny yw
Mae'r sgwâr mewnol wedi'i haneru yn yr un modd, a dim ond dau driongl a geir, felly mae'r prawf yn mynd yn ei flaen fel uchod heblaw am ffactor o , sy'n cael ei dynnu trwy luosi â dau i roi'r canlyniad.
Prawf gan ddefnyddio differynnau
[golygu | golygu cod]Gellir cyrraedd theorem Pythagoras trwy astudio sut mae newidiadau mewn ochr yn cynhyrchu newid yn yr hypotenws a hynny drwy ddefnyddio calcwlws.[17][18][19]
Mae'r triongl ABC yn driongl sgwâr, fel y dangosir yn rhan uchaf y diagram, gyda BC yn hypotenws. Ar yr un pryd mesurir hyd y triongl fel y dangosir, gyda'r hypotenws o hyd y, yr ochr AC o hyd x a'r ochr AB o hyd a, fel y gwelir yn y rhan diagram isod.

Os yw x yn cael ei gynyddu gan ychydig bach dx trwy ymestyn yr ochr AC ychydig tuag at D, yna mae y hefyd yn cynyddu gan dy. Mae'r rhain yn ffurfio dwy ochr triongl, CDE, sydd (gydag E wedi'i ddewis fel bod CE yn berpendicwlar i'r hypotenws) yn driongl sgwâr sy'n debyg iawn i ABC. Felly, rhaid i gymarebau eu hochrau fod yr un fath, hynny yw:
Gellir ailysgrifennu hyn fel , sy'n hafaliad gwahaniaethol y gellir ei ddatrys trwy integreiddio'n uniongyrchol:
sy'n rhoi
Gellir tynnu'r cysonyn o x = 0, y = a i roi'r hafaliad
Mae hyn yn fwy o brawf greddfol nag un ffurfiol: gellir ei wneud yn fwy trylwyr os defnyddir terfynau cywir yn lle dx a dy .
Cyfdro
[golygu | golygu cod]Mae'r theorem gyfdro (neu'r gwrthwyneb) hefyd yn wir:[20]
Ar gyfer unrhyw dri rhifau positif a, b, ac c fel bod a2 + b2 = c2, ceir tdriongl gydag ochrau a, b ac c, ac mae gan bob triongl p'i fath ongl sgwâr rhwng yr ochrau sydd a'u hyd yn a a b.
Datganiad arall fyddai'r canlynol:
Ar gyfer unrhyw driongl ag ochrau a, b, c, os yw a2 + b2 = c2, yna mae'r ongl rhwng a a b yn mesur 90°.
Mae gan driphlyg Pythagoras dri chyfanrif positif a, b, c fel bod a2 + b2 = c2. Mewn geiriau eraill, mae triphlyg Pythagoras yn cynrychioli hyd ochrau triongl sgwâr lle mae gan y tair ochr hydoedd cyfanrif (integer lengths).[21] Mae triphlyg o'r fath wedi'i ysgrifennu'n gyffredin fel (a, b, c). Ymhlith yr enghreifftiau adnabyddus y mae (3, 4, 5) a (5, 12, 13).
Canlyniadau a defnydd o'r theorem
[golygu | golygu cod]Triphlyg Pythagoras
[golygu | golygu cod]Mae triphlyg Pythagoras cyntefig yn un lle mae a, b ac c yn gydgysefin (coprime'); y rhannydd cyffredin mwyaf o a, b ac c yw 1).
Mae'r canlynol yn rhestr o driphlygion Pythagoras cyntefig gyda gwerthoedd llai na 100:
- (3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12, 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29), (28, 45, 53), (33, 56, 65), (36, 77, 85), (39, 80, 89), (48, 55, 73), (65, 72, 97)
Theorem Pythagoras cilyddol
[golygu | golygu cod]O ystyried triongl ongl sgwâr gydag ochrau ac uchder (llinell o'r ongl sgwâr ac yn berpendicwlar i'r hypotenws ). Mae gan theorem Pythagorean,
tra bod y theorem Pythagoras cilyddol [22] neu'r theorem Pythagorean wyneb i waered [23] yn cysylltu'r ddwy goes i'r uchder ,[24] yna
Gellir trawsnewid yr hafaliad i
lle mae ar gyfer unrhyw real nad yw'n sero. Os bydd yn gyfanrifau, yr ateb lleiaf yna bydd
gan ddefnyddio'r triphlyg Pythagoras lleiaf . Mae'r theorem Pythagoras cilyddol yn achos arbennig o'r hafaliad optig
lle mae'r enwaduron yn sgwariau a hefyd ar gyfer triongl heptagonal sydd a'i ochrau yn rhifau sgwâr.
Hyd anghymesur
[golygu | golygu cod]
Un o ganlyniad theorem Pythagoras yw y gellir llunio segmentau llinell y mae eu hyd yn anghymesur (felly nid yw'r gymhareb yn rhif cymarebolol) gan ddefnyddio pren mesur a chwmpawd. Mae theorem Pythagoras yn galluogi llunio hyd/oedd anghymesur oherwydd bod hypotenws triongl yn gysylltiedig â'r ochrau gan weithredu'r ail isradd.
Mae'r ffigur ar y dde yn dangos sut i lunio segmentau llinell y mae eu hyd yng nghymhareb ail isradd unrhyw gyfanrif positif.[25] Mae gan bob triongl ochr (wedi'i labelu "1") sef yr uned a ddewiswyd i'w mesur. Ym mhob triongl ongl sgwâr, mae theorem Pythagoras yn sefydlu hyd yr hypotenws o ran yr uned hon. Os yw'r hypotenws yn gysylltiedig â'r uned gan ail isradd cyfanrif positif nad yw'n sgwâr perffaith, mae'n sylweddoliad o hyd sy'n anghymesur â'r uned, fel √2, √3, √5 .
Rhifau cymhlyg
[golygu | golygu cod]
Ar gyfer unrhyw rif cymhlyg
rhoddir y gwerth absoliwt neu'r modwlws gan
Felly mae'r tri maint, r, x ac y yn gysylltiedig â hafaliad Pythagoras,
Sylwch fod r wedi'i ddiffinio i fod yn rhif positif neu'n sero ond gall x ac y fod yn negydd yn ogystal â bod yn bositif. Yn geometregol r yw pellter z o sero neu'r tarddiad O yn yr plân cymhlyg.
Gellir cyffredinoli hyn i ddarganfod y pellter rhwng dau bwynt, dywed z1 a z2. Rhoddir y pellter gofynnol gan
felly unwaith eto maent yn gysylltiedig â fersiwn o hafaliad Pythagoras,
Pellter Ewclidaidd
[golygu | golygu cod]Mae'r fformiwla pellter mewn cyfesurynnau Cartesaidd yn deillio o'r theorem Pythagoras.[26] Os yw (x1, y1) a (x2, y2) yn bwyntiau yn y plân, yna rhoddir y pellter rhyngddynt, a elwir hefyd yn bellter Ewclidaidd gan
Yn fwy cyffredinol, mewn n-gofod Euclidaidd, diffinnir y pellter Ewclidaidd rhwng dau bwynt, a , trwy gyffredinoli theorem Pythagoras, fel:
Os defnyddir sgwâr y gwerth hwn (y pellter Ewclidaidd sgwâr, neu SED) yn lle pellter Ewclidaidd, mae'r hafaliad sy'n deillio o hyn yn osgoi'r ail isradd ac yn syml mae'n swm o SED y cyfesurynnau:
Mae'r ffurf ail isradd yn ffwythiant llyfn, amgrwm o'r ddau bwynt, ac fe'i defnyddir yn helaeth mewn theori optimeiddio ac ystadegau, sy'n sail i'r 'sgwariau lleiaf'.
Pellter Ewclidaidd mewn systemau cyfesurynnau eraill
[golygu | golygu cod]Os na ddefnyddir cyfesurynnau Cartesaidd, er enghraifft, os defnyddir cyfesurynnau polar mewn dau ddimensiwn neu, yn fwy cyffredinol, os defnyddir cyfesurynnau cromliniol, mae'r fformwlâu sy'n mynegi'r pellter Ewclidaidd yn fwy cymhleth na theorem Pythagoras, ond gellir eu cael ohonynt. Gellir gweld enghraifft nodweddiadol lle mae'r pellter llinell syth rhwng dau bwynt yn cael ei drawsnewid yn gyfesurynnau cromliniol yng nghymwysiadau polynomialau Legendre mewn ffiseg a gellir darganfod y fformwlâu trwy ddefnyddio theorem Pythagoras gyda'r hafaliadau sy'n cysylltu'r cyfesurynnau cromliniol â chyfesurynnau Cartesaidd. Er enghraifft, gellir cyflwyno'r cyfesurynnau (r, θ) fel
Yna mae dau bwynt gyda lleoliadau (r1, θ1) a (r2, θ2) yn cael eu gwahanu gan bellter s :
Gan berfformio'r ail isradd a chyfuno termau, mae fformiwla Pythagoras ar gyfer pellter mewn cyfesurynnau Cartesaidd yn cynhyrchu'r gwahaniad mewn cyfesurynnau polar fel:
gan ddefnyddio'r fformwlâu trigonometrig cynnyrch-i-swm. Y fformiwla hon yw deddf cosin, a elwir weithiau yn "theorem Pythagoras cyffredinol".[27] O'r canlyniad hwn, ar gyfer yr achos lle mae'r radiws i'r ddau leoliad ar ongl sgwâr, mae'r ongl gaeedig Δθ = π/2, a'r ffurf sy'n cyfateb i theorem Pythagoras yn cael ei hadennill: Felly mae theorem Pythagoras, sy'n ddilys ar gyfer trionglau sgwar, yn achos arbennig o ddeddf fwy cyffredinol cosin, sy'n ddilys ar gyfer trionglau mympwyol.
Unfathiant trigonometrig Pythagoras
[golygu | golygu cod]
Mewn triongl ongl sgwâr gydag ochrau a, b a hypotenws c, mae trigonometreg yn pennu sin a chosin yr ongl θ rhwng ochr a a'r hypotenws fel:
O hynny mae'n dilyn:
lle mae'r cam olaf yn berthnasol i theorem Pythagoras. Weithiau gelwir y berthynas hon rhwng sin a cosin yn unfathiant sylfaenol trigonometrig Pythagoras.[28] Mewn trionglau tebyg, mae cymarebau'r ochrau yr un fath waeth beth yw maint y trionglau, ac yn dibynnu ar yr onglau.
Cyfeiriadau
[golygu | golygu cod]- ↑ Benson, Donald. The Moment of Proof : Mathematical Epiphanies, pp. 172–173 (Oxford University Press, 1999).
- ↑ "that the Greek literature which we possess belonging to the first five centuries after Pythagoras contains no statement specifying this or any other particular great geometric discovery to him."
- ↑ (Loomis 1968)
- ↑ (Maor 2007)
- ↑ 5.0 5.1 Stephen W. Hawking (2005). God created the integers: the mathematical breakthroughs that changed history. Philadelphia: Running Press Book Publishers. t. 12. ISBN 0-7624-1922-9. This proof first appeared after a computer program was set to check Euclidean proofs.
- ↑ Jan Gullberg (1997). Mathematics: from the birth of numbers. W. W. Norton & Company. t. 435. ISBN 0-393-04002-X.
- ↑ Elements 1.47 by Euclid. Retrieved 19 December 2006.
- ↑ Euclid's Elements, Book I, Proposition 47: web page version using Java applets from Euclid's Elements by Prof. David E. Joyce, Clark University
- ↑ The proof by Pythagoras probably was not a general one, as the theory of proportions was developed only two centuries after Pythagoras; see (Maor 2007)
- ↑ Alexander Bogomolny. "Pythagorean theorem, proof number 10". Cut the Knot. Cyrchwyd 27 Chwefror 2010.
- ↑ (Loomis 1968, Geometric proof 22 and Figure 123)
- ↑ Schroeder, Manfred Robert (2012). Fractals, Chaos, Power Laws: Minutes from an Infinite Paradise. Courier Corporation. tt. 3–4. ISBN 978-0486134789.
- ↑ Alexander Bogomolny. "Cut-the-knot.org: Pythagorean theorem and its many proofs, Proof #3". Cut the Knot. Cyrchwyd 4 Tachwedd 2010.
- ↑ Alexander Bogomolny. "Cut-the-knot.org: Pythagorean theorem and its many proofs, Proof #4". Cut the Knot. Cyrchwyd 4 Tachwedd 2010.
- ↑ Lantz, David. "Garfield's proof of the Pythagorean Theorem". Math.Colgate.edu. Archifwyd o'r gwreiddiol ar 2013-08-28. Cyrchwyd 2018-01-14.
- ↑ Maor, Eli, The Pythagorean Theorem, Princeton University Press, 2007: pp. 106-107.
- ↑ Mike Staring (1996). "The Pythagorean proposition: A proof by means of calculus". Mathematics Magazine (Mathematical Association of America) 69: 45–46. doi:10.2307/2691395. JSTOR 2691395. https://archive.org/details/sim_mathematics-magazine_1996-02_69_1/page/45.
- ↑ Bogomolny, Alexander. "Pythagorean Theorem". Interactive Mathematics Miscellany and Puzzles. Alexander Bogomolny. Archifwyd o'r gwreiddiol ar 2010-07-06. Cyrchwyd 2010-05-09.
- ↑ Bruce C. Berndt (1988). "Ramanujan – 100 years old (fashioned) or 100 years new (fangled)?". The Mathematical Intelligencer 10 (3): 24–31. doi:10.1007/BF03026638. https://archive.org/details/sim_mathematical-intelligencer_summer-1988_10_3/page/24.
- ↑ Judith D. Sally; Paul J. Sally Jr. (2007-12-21). "Theorem 2.4 (Converse of the Pythagorean theorem).". Roots to Research. American Mathematical Society. tt. 54–55. ISBN 978-0-8218-4403-8.
- ↑ Judith D. Sally; Paul Sally (2007). "Chapter 3: Pythagorean triples". Roots to research: a vertical development of mathematical problems. American Mathematical Society Bookstore. t. 63. ISBN 978-0-8218-4403-8.
- ↑ R. B. Nelsen, Proof Without Words: A Reciprocal Pythagorean Theorem, Mathematics Magazine, 82, December 2009, p. 370
- ↑ The upside-down Pythagorean theorem, Jennifer Richinick, The Mathematical Gazette, Vol. 92, No. 524 (July 2008), pp. 313-316
- ↑ Alexander Bogomolny, Pythagorean Theorem for the Reciprocals,https://www.cut-the-knot.org/pythagoras/PTForReciprocals.shtml
- ↑ Law, Henry (1853). "Corollary 5 of Proposition XLVII (Pythagoras's Theorem)". The Elements of Euclid: with many additional propositions, and explanatory notes, to which is prefixed an introductory essay on logic. John Weale. t. 49.
- ↑ Jon Orwant; Jarkko Hietaniemi; John Macdonald (1999). "Euclidean distance". Mastering algorithms with Perl. O'Reilly Media, Inc. t. 426. ISBN 1-56592-398-7.
- ↑ Wentworth, George (2009). Plane Trigonometry and Tables. BiblioBazaar, LLC. t. 116. ISBN 978-1-103-07998-8., Exercises, page 116
- ↑ Lawrence S. Leff (2005). PreCalculus the Easy Way (arg. 7th). Barron's Educational Series. t. 296. ISBN 0-7641-2892-2.


































































