Plân cymhlyg

Mewn mathemateg, mae'r plân cymhlyg neu plân-z yn gynrychiolaeth geometrig o'r rhifau cymhlyg a sefydlwyd gan yr echelin real a'r echelin ddychmygol berpendicwlar. Gellir ei ystyried fel plân Cartesaidd wedi'i addasu, gyda rhan real o rif cymhlyg, a gynrychiolir gan ddadleoliad ar hyd yr echelin-x, a rhan ddychmygol trwy ddadleoli ar hyd echelin-y. Ceir ystyron eraill i'r term plân cymhlyg, ond dyma'r ystyr mwyaf cyffredin.
Mae'r cysyniad o blân cymhlyg yn caniatáu dehongliad geometrig o rifau cymhlyg. O dan adio, maent yn adio fel fectorau. Gellir mynegi lluosi dau rif cymhlyg fel cyfesurynnau polar: maint (neu werth absoliwt) y lluoswm yw lluoswm y ddau werth absoliwt, a elwir hefyd yn "fodiwlau", ac ongl neu ymresymiad y lluoswm yw swm y ddau ongl, neu ymresymiad. Yn benodol, mae lluosi gyda rhif cymhlyg o fodiwlau, mae 1 yn gweithredu fel cylchdro.
Gelwir y plân weithiau'n "blân Argand".
Nodiant
[golygu | golygu cod]Mewn dadansoddiad cymhlyg, mae'r rhifau cymhlyg fel arfer yn cael eu cynrychioli gan y symbol z, a ellir ei wahanu'n ddwy ran rhifau real (x) a rhifau dychmygol (y):
er enghraifft: z = 4 + 5i, lle mae x a y yn rhifau real ac i yn uned ddychmygol. Yn y dull traddodiadol hwn mae'r rhif cymhlyg z yn cyfateb i'r pwynt (x, y) yn y plân Cartesaidd.
Yn y plân Cartesaidd, gellir mynegi'r pwynt (x, y) mewn cyfesurynnau polar fel
Yn y plân cymhlyg, mae'r cyfesurynnau polar yma'n cymryd y ffurf
lle
Diagram Argand
[golygu | golygu cod]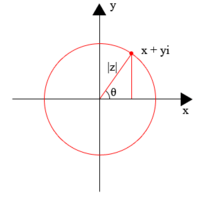
Mae'r term "Diagram Argand" fel arfer yn cyfeirio at blot geometrig o rifau cymhlyg, fel pwyntiau z=x+iy, gan ddefnyddio echelin-x fel yr echelin real ac echelin-y fel yr echeln ddychmygol.[1]. Enwyd y diagram ar ôl Jean-Robert Argand (1768–1822), er iddo gael ei ddisgrifio'n gyntaf gan Caspar Wessel (1745–1818).[2] Defnyddir y diagram yn aml i blotio safleoedd seros a phegynnau ffwythiant ar y plân cymhlyg.
Gweler hefyd
[golygu | golygu cod]Cyfeiriadau
[golygu | golygu cod]- ↑ W., Weisstein, Eric. "Argand Diagram". mathworld.wolfram.com. Cyrchwyd 19 Ebrill 2018.
- ↑ Cyflwynwyd bywgraffiad Wessel i Academi Dnmarc yn 1797; cyhoeddwyd papur Argand yn 1806. (Whittaker & Watson, 1927, t. 9)




