Perpendicwlar

Mewn geometreg dywedir fod un linell yn berpendicwlar i linell arall pan fo'r pan fo'r ddwy'n croesi ar ongl sgwâr (90 gradd). Mae'r gair 'perpendicwlar, felly, yn disgrifio perthynas dwy linell i'w gilydd.[2]
Gelwir y man lle mae'r ddwy linell yn cyfarfod hefyd yn 'groestoriad' - lle mae'r ddwy linell berpendicwlar yn torri ar draws ei gilydd. Mae dwy linell berpendicwlar yn creu cymesuredd. Mae hyn yn golygu fod y ddwy linell yn berpendicwlar i'w gilydd, yn yr un modd. Yn y diagram ar y dde, gellir dweud hefyd fod "llinell CD yn berpendicwlar i linell AB", ac nid oes trefn na hierarchiaeth i berpendicwlariaeth.
Gellir ymestyn hyn i segmentau llinellau a phelydrau. Mewn symbolau, mae yn nodi fod AB yn berpendicwlar i segment CD.[2] Gelwir y symbol hwn yn up tack.[2]
Creu perpendicwlar[golygu | golygu cod]
Mae'r cyfarwyddiadau isod yn cyd-fynd â'r diagram ar y chwith.
- Cam 1 (coch): lluniwch gylch, gyda'i ganolbwynt ar P, gan greu pwyntiau A' a B' ar y linel AB. Mae'r ddau bwynt yma (A' a B') yn gytbell o bwynt P.
- Cam 2 (gwyrdd): lluniwch ddwy gylch debyg (yr un radiws) - y naill o amgylch pwynt A' a'r llall o amgylch pwynt B'. Fe wnawn alw'r ddwy groesbwynt yn Q ac yn P.
- Cam 3 (glas): cysylltwch pwynt Q gyda phwynt P, gan lunio perpendicwlar perffaith!
Er mwyn profi bod yr PQ yn berpendicwlar i AB (a'r ffordd arall!), gellir defnyddio damcaniaeth cyfathiant trionglau (Congruence of triangles neu "ochr-ochr-ochr") ar gyfer ' a QPB' er mwyn dod i'r casgliad bod onglau OPA' ac OPB' yn gyfartal. Defnyddir yr un ddamcaniaeth eilwaith ar gyfer trionglau OPA' ac OPB' gan ddo i'r casgliad terfynol fod onglau POA a POB yn hafal i'w gilydd.
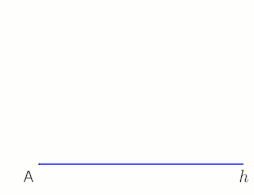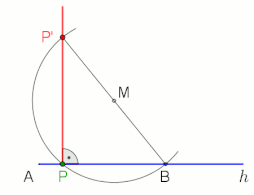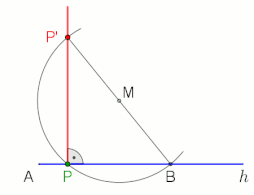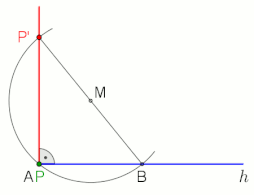
Er mwyn llunio perpendicwlar i linell g drwy (neu ar) bwynt P, gellir defnyddio damcaniaeth Thales, gweler yr animeiddiad ar y dde.
Gellir, hefyd, defnyddio Theorem Pythagoras fel sail i lunio ongl sgwâr (ac yn ei sgil, y perpendicwlar). Er enghraifft, drwy gyfri dolennau cadwyn tair rhan: tair dolen yn y cyntaf, pedair yn yr ail a phump yn y trydydd (3:4:5) gellir eu gosod yn wastad i ffurfio triongl hafalochrog, gyda'r ongl sgwâr gyferbyn a'r gadwen hiraf (5 dolen). Defnyddir y dull hwn ers cyn cof, gan adeiladwyr y pyramidiau, a sawl gwareiddiad arall, yn enwedig pan fo angen perpendicwlar, neu ongl sgwâr ar raddfa fawr ee cynllunio gerddi, caeau, pyramid neu adeilad.
Ffwythiannau graff[golygu | golygu cod]
Yn y plân dau ddimensiwn, gellir llunio onglau sgwâr gan ddwy linell sy'n croestori os yw lluoswm eu goleddau (slopes) yn hafal i -1. Felly, mae diffinio Ffwythiant llinol: y1 = a1x + b1 a y2 = a2x + b2, mae graff y ffwythiannau'n berpendicwlar, ac yn creu pedwar ongl sgwâr, ble mae'r llinellau'n croestorri os yw a1a2 = −1. Fodd bynnag, ni ellir defnyddio'r dull hwn os yw'r goleddau'n sero, neu heb eu diffinio (h.y. mae'r linell yn gyfochrog i echelin).
Ceir dull arall: boed i'r ddau ffwythiant llinol fod yn: a1x + b1y + c1 = 0 ac a2x + b2y + c2 = 0. Bydd y llinellau'n berpendicwlar os (a dim ond os) yw a1a2 + b1b2 = 0.