Trigonometreg

Mae "Trigonometreg" yn ailgyfeirio i'r erthygl hon. Am ddefnyddiau eraill, gweler Trigonometreg (gwahaniaethu).

Trigonometreg

Enghraifft o'r canlynol	maes o fewn mathemateg
Math	geometreg
Ffeiliau perthnasol ar Gomin Wicimedia

Rheolau Syml Trig

Mae trigonometreg (Groeg: τρίγωνον "triongl" + μέτρον "mesur") yn gangen o fathemateg sy'n delio gyda hyd ochrau ac onglau thrionglau, yn enwedig y trionglau ongl sgwâr. Gelwir trigonometreg yn "trig" yn anffurfiol. Mae trigonometreg yn delio gyda'r berthynas rhwng ochrau a'r onglau a'r ffwythiannau trigonometregol sy'n disgrifio'r perthnasau hynny.

Mae gan drigonometreg gymwysiadau mewn mathemateg bur ac mewn mathemateg gymhwysol, ac ystyrir y ddisgyblaeth hon yn anghenrheidiol o fewn nifer o ganghennau o wyddoniaeth a thechnoleg. Câi ei dysgu mewn ysgolion uwchradd fel naill ai cwrs ar wahân neu fel rhan o gwrs cyn-galcwlws.

Gall yr holl ffwythiannau trigonometregol ongl θ gael eu creu yn geometregol yn nhermau cylch unedol o amgylch O.

Y ffwythiannau sin(x) a cos(x) wedi'u graffio

Daeth y maes i'r amlwg yn yr oes Helenistaidd yr ystod y 3g CC o gymhwyso geometreg ac meysydd eraill megis astudiaethau seryddol. Canolbwyntiodd y Groegiaid ar gyfrifo "cordiau" (e.e. Almagest Ptolemi), tra chreodd mathemategwyr India y tablau gwerthoedd cynharaf y gwyddys amdanynt ar gyfer cymarebau trigonometrig, a elwir hefyd yn swyddogaethau trigonometrig ee sin.[3]

Trwy gydol hanes, cymhwyswyd trigonometreg mewn meysydd fel geodesi, tirfesur, mecaneg nefol, a fforio.

Mae trigonometreg yn adnabyddus am ei unfathiannau trigonometrig a ddefnyddir yn aml ar gyfer ailysgrifennu ymadroddion trigonometreg gyda'r nod o symleiddio'r mynegiad, dod o hyd i ffurf fwy defnyddiol o fynegiant, neu i ddatrys hafaliad.

Gofod metrig

Mae trigonometreg yn un disgyblaeth oddi fewn i Ofod:

Geometreg	Trigonometreg	Geometreg Gwahaniaethol	Topoloeg	Geometreg ffractalaidd	Theori mesuredd

Hanes

Credir maiHipparchus, a luniodd y tabl trigonometrig cyntaf, ac oherwydd hyn, adnabyddir ef fel "tad trigonometreg".[8] Myn eraill mai Nasir al-Din al-Tusi mathemategydd o Bersia yw tad go-iawn trigonometreg.

Astudiodd seryddwyr Swmeraidd fesur onglau, gan ddefnyddio rhanu'r cylch yn 360 gradd. Fe astudio nhw (ac yn ddiweddarach y Babiloniaid) gymarebau ochrau trionglau cyflun (tebyg) a darganfod rhai priodweddau'r cymarebau hyn, ond ni wnaethant droi hynny'n ddull systematig ar gyfer dod o hyd i ochrau ac onglau trionglau. Defnyddiodd yr Nwbiaid hynafol ddull tebyg.

Yn y 3g CC, astudiodd rhai mathemategwyr Helenistaidd fel Euclid ac Archimedes briodweddau cordiau ac onglau arysgrifedig mewn cylchoedd, a phrofwyd theoremausy'n cael eu hadnabod heddiw fel fformwlâu trigonometrig modern, er eu bod yn eu cyflwyno yn geometregol yn hytrach nag yn algebraidd. Yn 140 CC, rhoddodd Hipparchus (o Nicaea, Asia Leiaf) y tablau cyntaf o gordiau, sy'n cyfateb i dablau modern o werthoedd sin at ei gilydd, a'u defnyddio i ddatrys problemau mewn trigonometreg a thrigonometreg sfferig. [11] Yn yr 2g OC, lluniodd y seryddwr Groegaidd-Eifftaidd Ptolemi (o Alexandria, yr Aifft) dablau trigonometrig manwl ("tabl cordiau Ptolemi") yn Llyfr 1, pennod 11 o'i Almagest. Defnyddiodd Ptolemi hyd cord i ddiffinio ei swyddogaethau trigonometrig, sy'n eithriadol o debyg i'r confensiwn sin a ddefnyddiwn heddiw.[13]

Aeth canrifoedd heibio cyn cynhyrchu tablau manylach, ac defnyddiwyd traethawd Ptolemi ar gyfer perfformio cyfrifiadau trigonometrig mewn seryddiaeth trwy gydol y 1,200 mlynedd nesaf yn y gwledydd Bysantaidd, Islamaidd, ac yn ddiweddarach, Gorllewin Ewrop.

Ardystiwyd y confensiwn sin modern gyntaf yn y Surya Siddhanta, sef erthygl Sansgrit o'r 15g, a chofnodwyd ei briodweddau ymhellach gan fathemategydd a seryddwr Indiaidd y 5g (OC) o'r enw Aryabhata.[14] Cyfieithwyd ac ehangwyd y gweithiau Groegaidd ac Indiaidd hyn gan fathemategwyr Islamaidd canoloesol. Erbyn y 10g, roedd mathemategwyr Islamaidd yn defnyddio pob un o'r chwe swyddogaeth trigonometrig, wedi tablu eu gwerthoedd, ac yn eu cymhwyso i broblemau mewn geometreg sfferig. Disgrifiwyd y polymath Persiaidd Nasir al-Din al-Tusi fel crëwr trigonometreg fel disgyblaeth fathemategol ynddo'i hun. Nasīr al-Dīn al-Tūsī oedd y cyntaf i drin trigonometreg fel disgyblaeth fathemategol yn annibynnol ar seryddiaeth, a datblygodd trigonometreg sfferig i'w ffurf bresennol. Rhestrodd y chwe achos gwahanol o driongl ongl sgwâr mewn trigonometreg sfferig, ac yn ei Ffigur ar y Sector, nododd ddeddfau sin ar gyfer trionglau plân a thrionglau sfferig; darganfu gyfraith tangiadau ar gyfer trionglau sfferig, ac yn bennaf, darparodd brofion ar gyfer y deddfau hyn.

Cyrhaeddodd gwybodaeth am ffwythiannau a dulliau trigonometrig Orllewin Ewrop trwy gyfieithiadau i'r Lladin o Almagest Groegaidd Ptolemi yn ogystal â gweithiau seryddwyr Persiaidd ac Arabaidd fel Al Battani a Nasir al-Din al-Tusi.[22] Un o'r gweithiau cynharaf ar trigonometreg gan fathemategydd yng ngogledd Ewrop yw De Triangulis gan y mathemategydd Almaeneg Regiomontanus o'r 15g, a gafodd ei annog i ysgrifennu, a darparu copi o'r Almagest, gan yr ysgolhaig Groegaidd Bysantaidd Basilios Bessarion a bu'r ddau'n cyd-fyw am sawl blwyddyn gyda'i gilydd. Ar yr un pryd, cwblhawyd cyfieithiad arall o'r Almagest o'r Groeg i'r Lladin gan fathemategydd o Greta (fwyaf o ynysoedd Gwlad Groeg) George o Trebizond. Ychydig iawn o wybodaeth oedd wedi cyrraedd Ewrop, hyd nes iNicolaus Copernicus neilltuo dwy bennod o De revolutionibus orbium coelestium i egluro ei gysyniadau sylfaenol.

Wedi'i sbarduno gan ofynion mordwyo a'r angen cynyddol am fapiau cywir o ardaloedd daearyddol mawr, tyfodd trigonometreg yn gangen fawr o fathemateg yn Ewrop hefyd. Bartholomaeus Pitiscus oedd y cyntaf i ddefnyddio'r gair, gan gyhoeddi ei Trigonometria ym 1595. Disgrifiodd Gemma Frisius am y tro cyntaf y dull triongli (triangulation) sy'n dal i gael ei ddefnyddio hyd heddiw wrth fesur tir. Leonhard Euler a ymgorfforodd rifau cymhlyg i fewn i digonometreg. Roedd gweithiau mathemategwyr yr Alban - James Gregory yn yr 17g a Colin Maclaurin yn y 18g - yn ddylanwadol yn natblygiad cyfresi trigonometrig. Hefyd yn y 18g, diffiniodd Brook Taylor gyfres gyffredinol Taylor.

Cymarebau trigonometrig

Yn y triongl sgwâr hwn: sin A = a / c ; cos A = b / c ; tan A = a / b .

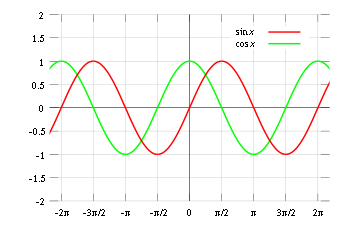
Cymarebau trigonometrig yw'r cymarebau rhwng ymylon y triongl sgwâr. Rhoddir y cymarebau hyn gan y ffwythiannau trigonometrig canlynol o'r ongl hysbys A, lle mae a, b ac c yn cyfeirio at hyd yr ochrau yn y ffigur sy'n cyd-fynd:

• Ffwythiant Sine (sin), a ddiffinnir fel cymhareb yr ochr gyferbyn ag ongl yr hypotenws.

$\sin A={\frac {\textrm {opposite}}{\textrm {hypotenuse}}}={\frac {a}{c}}.$

• Ffwythiant cosin (cos), a ddiffinnir fel cymhareb y goes gyfagos (ochr y triongl sy'n ymuno â'r ongl i'r ongl sgwâr) i'r hypotenws.

$\cos A={\frac {\textrm {adjacent}}{\textrm {hypotenuse}}}={\frac {b}{c}}.$

• Ffwythiant tangiad (tan), a ddiffinnir fel cymhareb y goes gyferbyn â'r goes gyfagos.

$\tan A={\frac {\textrm {opposite}}{\textrm {adjacent}}}={\frac {a}{b}}={\frac {a/c}{b/c}}={\frac {\sin A}{\cos A}}.$

Y hypotenws yw'r ochr gyferbyn â'r ongl 90 gradd mewn triongl sgwâr; hi yw ochr hiraf y triongl ac un o'r ddwy ochr wrth ymyl ongl A. Y goes gyfagos yw'r ochr arall sy'n gyfagos i ongl A. Yr ochr arall yw'r ochr sydd gyferbyn ag ongl A. Weithiau defnyddir y termau perpendicwlar a sylfaen ar gyfer yr ochrau cyferbyniol a chyfagos. Gweler isod o dan Mnemonics.

Gan fod unrhyw ddwy driongl sgwâr (sydd â'r un ongl lem A) yn debyg, mae gwerth y gymhareb trigonometrig yn dibynnu ar ongl A yn unig .

Enwau cilyddol y ffwythiannau hyn yw cosecant (csc), secant (sec), a cotangent (cot), yn y drefn honno:

$\csc A={\frac {1}{\sin A}}={\frac {\textrm {hypotenuse}}{\textrm {opposite}}}={\frac {c}{a}},$

$\sec A={\frac {1}{\cos A}}={\frac {\textrm {hypotenuse}}{\textrm {adjacent}}}={\frac {c}{b}},$

$\cot A={\frac {1}{\tan A}}={\frac {\textrm {adjacent}}{\textrm {opposite}}}={\frac {\cos A}{\sin A}}={\frac {b}{a}}.$

Mae cosin, cotangent, a cosecant yn cael eu henwi felly oherwydd eu bod yn y drefn honno yn sin, tangiad, a secant yr ongl gyflenwol sydd wedi'i dalfyrru i "cyd-".

Gyda'r ffwythiannau hyn, gellir ateb bron pob cwestiwn am drionglau mympwyol trwy ddefnyddio deddf sin a deddf cosin. Gellir defnyddio'r deddfau hyn i gyfrifo'r onglau ac ochrau sy'n weddill o unrhyw driongl cyn gynted ag y bydd dwy ochr a'u ongl gynhwysol neu ddwy ongl ac ochr neu dair ochr yn hysbys.

Cofyddiaeth (Mnemonics)

Defnydd cyffredin o mnemonics yw cymorth i gofio ffeithiau a pherthnas mewn trigonometreg. Er enghraifft, gellir cofio'r cymarebau sin, cosin, a thangiad mewn triongl dde trwy eu cynrychioli nhw a'u hochrau cyfatebol fel rhaff o lythrennau. Er enghraifft, mnemonig yw SOH-CAH-TOA:

S ine = O pposite ÷ H ypotenuse

C osine = A gyfagos ÷ H ypotenuse

T angent = O pposite ÷ A cyfagos

Y cylch fel uned a gwerthoedd trigonometrig cyffredin

Ffig. 1a - Sin a chosin ongl θ wedi'i ddiffinio gan ddefnyddio'r cylch uned.

Gellir cynrychioli cymarebau trigonometrig hefyd gan ddefnyddio'r uned y cylch, sef cylch radiws 1 wedi'i ganoli ar darddiad y plaân. Yn y gosodiad hwn, bydd ochr-derfyn ongl A wedi'i gosod mewn yn y safle arferol, yn croestorri'r uned y cylch ar bwynt (x, y), lle $x=\cos A$ a $y=\sin A$. Mae'r gynrychiolaeth hon yn caniatáu cyfrifo gwerthoedd trigonometrig cyffredin, fel y rhai yn y tabl canlynol:

Ffwythiant	0	$\pi /6$	$\pi /4$	$\pi /3$	$\pi /2$	$2\pi /3$	$3\pi /4$	$5\pi /6$	$\pi$
sin	$0$	$1/2$	${\sqrt {2}}/2$	${\sqrt {3}}/2$	$1$	${\sqrt {3}}/2$	${\sqrt {2}}/2$	$1/2$	$0$
cosine	$1$	${\sqrt {3}}/2$	${\sqrt {2}}/2$	$1/2$	$0$	$-1/2$	$-{\sqrt {2}}/2$	$-{\sqrt {3}}/2$	$-1$
tangiad	$0$	${\sqrt {3}}/3$	$1$	${\sqrt {3}}$	anniffiniedig	$-{\sqrt {3}}$	$-1$	$-{\sqrt {3}}/3$	$0$
secant	$1$	$2{\sqrt {3}}/3$	${\sqrt {2}}$	$2$	anniffiniedig	$-2$	$-{\sqrt {2}}$	$-2{\sqrt {3}}/3$	$-1$
cosecant	anniffiniedig	$2$	${\sqrt {2}}$	$2{\sqrt {3}}/3$	$1$	$2{\sqrt {3}}/3$	${\sqrt {2}}$	$2$	anniffiniedig
cotangent	anniffiniedig	${\sqrt {3}}$	$1$	${\sqrt {3}}/3$	$0$	$-{\sqrt {3}}/3$	$-1$	$-{\sqrt {3}}$	anniffiniedig

Ffwythianau trigonometrig newidynnau real neu gymhlyg

Gan ddefnyddio uned y cylch, gellir ymestyn y diffiniadau o gymarebau trigonometrig i bob dadl gadarnhaol a negyddol (gweler ffwythiannau trigonometrig).

Graffiau o ffwythianau trigonometrig

Mae'r tabl canlynol yn crynhoi priodweddau graffiau'r chwe phrif ffwythiant trigonometrig:

Ffwythiant	Cyfnod	Parth	Ystod	Graff
sin	$2\pi$	$(-\infty ,\infty )$	$[-1,1]$	</img>
cosin	$2\pi$	$(-\infty ,\infty )$	$[-1,1]$	</img>
tangiad	$\pi$	$x\neq \pi /2+n\pi$	$(-\infty ,\infty )$	</img>
secant	$2\pi$	$x\neq \pi /2+n\pi$	$(-\infty ,-1]\cup [1,\infty )$	</img>
cosecant	$2\pi$	$x\neq n\pi$	$(-\infty ,-1]\cup [1,\infty )$	</img>
cotangent	$\pi$	$x\neq n\pi$	$(-\infty ,\infty )$	</img>

Ffwythiant trigonometrig gwrthdro

Gan fod y chwe phrif ffwythiant trigonometrig yn gyfnodol, nid ydyn nhw'n ddyfeisgar (injective; neu, 1 i 1), ac felly nid ydyn nhw'n wrthdroadwy. Trwy gyfyngu parth ffwythiant trigonometrig, fodd bynnag, gellir eu gwneud yn wrthdroadwy.

Gellir gweld enwau'r ffwythiannau trigonometrig gwrthdro, ynghyd â'u parthau a'u hystod, yn y tabl canlynol:

Enw	Nodiant arferol	Diffiniad	Parth x ar gyfer canlyniad go iawn	Ystod o'r prif werth arferol (radianau)	Ystod o'r prif werth arferol (graddau)
arcsin	y = arcsin(x )	x = sin ( y )	−1 ≤ x ≤ 1	-  ≤ y ≤	−90 ° ≤ y ≤ 90 °
arccosin	y = arccos(x )	x = cos ( y )	−1 ≤ x ≤ 1	0 ≤ y ≤ π	0 ° ≤ y ≤ 180 °
arctangent	y = arctan(x )	x = tan ( y )	pob rhif real	-  < y <	−90 ° < y <90 °
arccotangent	y = arccot(x )	x = cot ( y )	pob rhif real	0 < y < π	0 ° < y <180 °
arcsecant	y = arcsec(x )	x = sec ( y )	x ≤ −1 neu 1 ≤ x	0 ≤ y <  neu  < y ≤ π	0 ° ≤ y <90 ° neu 90 ° < y ≤ 180 °
arccosecant	y = arccsc(x )	x = csc ( y )	x ≤ −1 neu 1 ≤ x	-  ≤ y <0 neu 0 < y ≤	−90 ° ≤ y <0 ° neu 0 ° < y ≤ 90 °

Cynrychioliadau cyfresi pŵer

Pan gânt eu hystyried fel ffwythiannau newidyn real, gellir cynrychioli'r cymarebau trigonometrig gan gyfres anfeidrol. Er enghraifft, mae gan sin a chosin y cynrychioladau canlynol:

${\begin{aligned}\sin x&=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots \\&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{(2n+1)!}}\\\end{aligned}}$

${\begin{aligned}\cos x&=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\cdots \\&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n}}{(2n)!}}.\end{aligned}}$

Gyda'r diffiniadau hyn gellir diffinio'r swyddogaethau trigonometrig ar gyfer rhifau cymhlyg. Pan gaiff ei ymestyn fel ffwythiannau newidynnau real neu gymhleth, mae'r fformiwla ganlynol yn gywir ar gyfer yr esbonyddol cymhlyg:

$e^{x+iy}=e^{x}(\cos y+i\sin y).$

Mae'r ffwythiant esbonyddol gymhlyg hon, a ysgrifennwyd o ran ffwythiannau trigonometrig, yn arbennig o ddefnyddiol mewn mathemateg.

Cyfrifo ffwythiannau trigonometrig

Roedd ffwythiannau trigonometrig ymhlith y defnyddiau cynharaf ar gyfer tablau mathemategol. Ymgorfforwyd tablau o'r fath mewn gwerslyfrau mathemateg a dysgwyd myfyrwyr i edrych ar werthoedd a sut i ryngosod rhwng y gwerthoedd a restrir i gael cywirdeb uwch. Roedd gan y Llithriwl raddfeydd arbennig ar gyfer ffwythiannau trigonometrig.

Mae gan gyfrifianellau gwyddonol fotymau ar gyfer cyfrifo'r prif swyddogaethau trigonometrig (sin, cos, tan, ac weithiau cis a'u gwrthdroadau). Mae'r mwyafrif o gyfrifianellau'n caniatáu dewis o ddulliau mesur ongl: graddau, radianau, ac weithiau graddyddion . Mae'r mwyafrif o ieithoedd rhaglennu cyfrifiadurol yn darparu llyfrgelloedd o ffwythiannau sy'n cynnwys y ffwythiannau trigonometrig.

Ceisiadau

Seryddiaeth

Am ganrifoedd, defnyddiwyd trigonometreg sfferig ar gyfer lleoli safleoedd yr haul, lleuad a'r ser, darogan eclipsau, ac yn disgrifio taith y planedau.

Yn y cyfnod modern, defnyddir y dechneg triongli (triangulation) mewn seryddiaeth i fesur y pellter i sêr cyfagos, yn ogystal ag mewn systemau llywio lloeren.

Fforio

Defnyddir y secstant i fesur ongl yr haul neu'r sêr mewn perthynas â'r gorwel. Gan ddefnyddio trigonometreg a chronomedr morol, gellir pennu lleoliad y llong o fesuriadau o'r fath.

Yn hanesyddol, defnyddiwyd trigonometreg ar gyfer lleoli lledred a hydred llongau hwylio, plotio cyrsiau, a chyfrifo pellteroedd wrth fordwyo.

Mae trigonometreg yn dal i gael ei ddefnyddio wrth fordwyo trwy ddulliau fel y System Lleoli Byd-eang a deallusrwydd artiffisial ar gyfer cerbydau diyrrwr.

Mesur tir

Wrth fesur y tir, defnyddir trigonometreg wrth gyfrifo hyd, arwynebedd ac onglau cymharol rhwng gwrthrychau.

Ar raddfa fwy, defnyddir trigonometreg mewn daearyddiaeth i fesur pellteroedd rhwng tirnodau.

Ffwythiannau cyfnodol

Ffwythiant $s(x)$ (mewn coch) yw swm o chwe ffwythiant sin o wahanol argiau (neu osgledau; amplitudau) ac amleddau sy'n cysylltiedig. Gelwir eu crynhoad yn gyfres Fourier. Y trawsnewidiad Fourier, $S(f)$ (mewn glas), sy'n darlunio osgled yn erbyn amledd, yn datgelu'r 6 amledd.

Darllen pellach

•  
• Linton, Christopher M. (2004). O Eudoxus i Einstein: Hanes Seryddiaeth Fathemategol . Gwasg Prifysgol Caergrawnt.
• Weisstein, Eric W. "Trigonometric Addition Formulas". MathWorld.

Dolenni allanol

• Academi Khan: Trigonometreg, micro-ddarlithoedd ar-lein am ddim
• Trigonometreg gan Alfred Monroe Kenyon a Louis Ingold, The Macmillan Company, 1914. Mewn delweddau, testun llawn wedi'i gyflwyno.
• Pos Trigonometreg Benjamin Banneker adeg Cydgyfeirio
• Cwrs Byr Dave mewn Trigonometreg gan David Joyce o Brifysgol Clark
• Trigonometreg, gan Michael Corral, Yn ymdrin â thrigonometreg elfennol, Wedi'i ddosbarthu o dan Drwydded Dogfennaeth Rydd GNU