Ongl
 | |
| Math | geometric object, two-dimensional object |
|---|---|
| Yn cynnwys | angular measure |
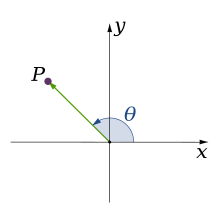
Mewn geometreg Ewclidaidd, ongl yw'r ffigur a ffurfir gan ddwy linell, o'r enw ochrau'r ongl, sy'n rhannu pwynt terfyn cyffredin, a elwir yn fertig yr ongl.[1] Mae onglau a ffurfiwyd gan ddau belydr (neu ddwy linell) yn gorwedd yn y plân sy'n cynnwys y llinellau. Ffurfir onglau hefyd trwy groesdorri dau blân: gelwir y rhain yn onglau deuhedrol. Mae dwy gromlin croestoriadol yn diffinio ongl hefyd, sef ongl y tangiadau ar y pwynt croestoriad. Er enghraifft, mae'r ongl sfferig a ffurfir gan ddau gylch mawr ar sffêr yn hafal i'r ongl deuhedroll rhwng y plannau sy'n cynnwys y cylchoedd mawr. delwedd gan y cylchdro.[2]
Mae'r ongl hefyd yn fesuriad o gylchdroad, y gymhareb o hyd arc i'w radiws. Y mesur hwn yw'r gymhareb o hyd arc crwn i'w radiws. Yn achos ongl geometrig, mae'r arc wedi'i ganoli yn y fertig ac wedi'i amffinio gan yr ochrau. Yn achos cylchdro, mae'r arc wedi'i ganoli yng nghanol y cylchdro a'i amffinio gan unrhyw bwynt arall a'i d
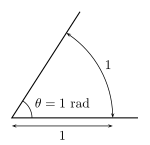
Mesurir onglau yn aml mewn graddau (°), ond y radian yw'r uned safonol. Ceir 360° mewn un troad cylch, a 2π radian mewn un troad cylch.[3] Gellir mesur onglau gydag onglydd. Defnyddir y llythyren Roeg theta (θ) fel symbol mathemategol am ongl.
Mathau[golygu | golygu cod]
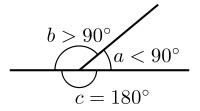


- Ongl sgwâr
Ongl sydd rhwng dwy linell bependicwlar; chwarter troad cylch; hanner ongl syth.
- Ongl lem
Ongl sy'n llai nag ongl sgwâr.
- Ongl aflem
Ongl sy'n fwy nag ongl sgwâr ond yn llai nag ongl syth.
- Ongl syth
Yr ongl sydd gan linell syth; hanner troad cylch; dwbl ongl sgwâr.
- Ongl atblyg neu allblyg
Ongl sy'n fwy nag ongl syth ond yn llai nag un troad cylch.
- Ongl lawn
Un troad cylch; dwy ongl syth; pedair ongl sgwâr.
- Onglau cyflenwol
Dwy ongl sy'n ffurfio ongl sgwâr.
- Onglau atodol
Dwy ongl sy'n ffurfio ongl syth.
Hanes ac etymoleg[golygu | golygu cod]
Daw'r gair ongl o'r gair Lladin angulus, sy'n golygu "cornel"; geiriau cytras yw'r Groeg ἀγκύλος (ankylοs), sy'n golygu "cam, crwm," a'r gair Saesneg "ankle", sef migwrn. Mae'r ddau yn gysylltiedig â'r gwreiddyn Proto-Indo-Ewropeaidd * ank-, sy'n golygu "i blygu" neu "bwa".[4] Dyma darddiad yr enw 'Ancr', sef math o feudwy, a blygai mewn gweddi, fel yn yr enw Llyfr Ancr Llanddewibrefi, sef llawysgrif a sgwennwyd yn 1346.
Mae'r mathemategydd Groegaidd Euclid yn diffinio ongl plân fel tueddiad at ei gilydd, mewn plân, o ddwy linell sy'n cwrdd â'i gilydd, ac nad ydyn nhw'n gorwedd yn syth mewn perthynas â'i gilydd. Yn ôl Proclus, rhaid i ongl fod naill ai'n ansawdd neu'n faint, neu'n berthynas. Defnyddiwyd y cysyniad cyntaf gan Eudemus, a oedd yn ystyried ongl fel gwyriad o linell syth ; yr ail gan Carpus o Antioch, a oedd yn ei ystyried fel yr egwyl neu'r gofod rhwng y llinellau croestoriadol; Mabwysiadodd Euclid y trydydd diffiniad.[5]
Adnabod onglau[golygu | golygu cod]

Mewn mynegiadau mathemategol, mae'n gyffredin defnyddio llythrennau Groeg (α, β, γ, θ, φ . . ) fel newidynnau sy'n dynodi maint ongl (er mwyn osgoi dryswch â'i ystyr arall, π at y diben hwn). Defnyddir hefyd y llythrennau bach Rhufeinig (a , b , c. . . ) hefyd yn cael eu defnyddio, a llythrennau Rhufeinig bras wrth drafod polygonau. Gweler y ffigurau yn yr erthygl hon am enghreifftiau.
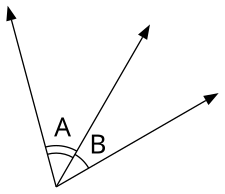
Mewn ffigurau geometrig, gellir adnabod onglau hefyd gan y labeli sydd ynghlwm wrth y tri phwynt sy'n eu diffinio. Er enghraifft, mae'r ongl yn fertig A wedi'i hamgáu gan y pelydrau AB ac AC (hy y llinellau o bwynt A i bwynt B a phwynt A i bwynt C) wedi'i dynodi'n ∠BAC. Lle nad oes risg o ddryswch, weithiau gellir cyfeirio at yr ongl yn syml gan ei fertig ("ongl A" yn yr achos hwn).
O bosibl, gallai ongl a ddynodir fel, dyweder, ∠BAC, gyfeirio at unrhyw un o bedair ongl: yr ongl clocwedd o B i C, yr ongl gwrthglocwedd o B i C, yr ongl clocwedd o C i B, neu'r ongl gwrthglocwedd o C i B, lle mae'r cyfeiriad y mae'r ongl yn cael ei fesur yn pennu ei arwydd. Fodd bynnag, mewn llawer o sefyllfaoedd geometregol, mae'n amlwg o'r cyd-destun mai'r ongl gadarnhaol sy'n llai na neu'n hafal i 180 gradd yw, ac os felly nid oes amwysedd yn codi. Fel arall, gellir mabwysiadu confensiwn fel bod ∠BAC bob amser yn cyfeirio at yr ongl gwrthglocwedd (positif) o B i C, ac ∠CAB yr ongl gwrthglocwedd (positif) o C i B.
Mathau o onglau[golygu | golygu cod]
Parau o onglau cywerth[golygu | golygu cod]
- Dywedir bod onglau sydd â'r un mesur (hy yr un maint) yn gyfartal, yn hafal neu'n gyfath. Diffinnir ongl yn ôl ei fesur ac nid yw'n dibynnu ar hyd ochrau'r ongl (ee mae pob ongl sgwâr yn hafal o ran mesur).
- Gelwir dwy ongl sy'n rhannu ochrau terfynell, ond sy'n wahanol o ran maint gan luosrif cyfanrif tro, yn onglau cyd-derfynol.
- Ongl cyfeiriol yw fersiwn lem unrhyw ongl a bennir trwy dynnu neu ychwanegu ongl syth dro ar ôl tro (1/2 tro, 180°, neu radianau π) at y canlyniadau yn ôl yr angen, hyd nes y bydd maint y canlyniad yn ongl lem, a gwerth rhwng 0 a 1/4 tro, 90°, neu π/2 radian. Er enghraifft, mae gan ongl 30 gradd ongl gyfeirio o 30 gradd, ac mae gan ongl o 150 gradd ongl gyfeirio o 30 gradd (80-150). Mae gan ongl o 750 gradd ongl gyfeirio o 30 gradd (750-720).[6]
Parau ongl fertigol a chyfagos[golygu | golygu cod]
Pan fydd dwy linell syth yn croestorri ar bwynt, ffurfir pedair ongl. Enwir yr onglau hyn yn ôl eu lleoliad mewn perthynas â'i gilydd.
- Gelwir pâr o onglau gyferbyn â'i gilydd, a ffurfiwyd gan ddwy linell syth sy'n croestorri sy'n ffurfio siâp tebyg i "X", yn onglau fertigol neu onglau gyferbyn neu'n onglau gyferbyn fertigol. Maent yn cael eu talfyrru fel fert. gwrth. ∠s neu yn Saesneg vert. opp. ∠s.[7]
- Gelwir cydraddoldeb onglau ferticol, gyferbyn yn theorem ongl fertigol. Priodolodd Eudemus of Rhodes y prawf i Thales of Miletus.[8][9] Dangosodd y cynnig, gan fod y ddau bâr o onglau fertigol yn atodol i'r ddwy ongl gyfagos, bod yr onglau fertigol yn gyfartal o ran mesur. Yn ôl cofnod hanesyddol,[9] pan ymwelodd Thales â'r Aifft, sylwodd eu bod yn mesur yr onglau fertigol i sicrhau eu bod yn gyfartal, i wiro'r gwaith, pob tro y byddai'r Eifftiaid yn tynnu dwy linell groestoriadol. Daeth Thales i'r casgliad y gallai rhywun brofi bod pob ongl fertigol yn gyfartal pe bai rhywun yn derbyn rhai syniadau cyffredinol fel:
- Mae pob ongl syth yn gyfartal.
- Mae hafaliadau sy'n cael eu hychwanegu at hafaliaid yn gyfartal.
- Mae hafaliadau a dynnwyd o hafal yn gyfartal.
- Talfyrrir onglau cyfagos, yn aml fel adj. ∠s, ac mae'r onglau yn onglau sy'n rhannu fertig ac ymyl cyffredin ond nad ydyn nhw'n rhannu unrhyw bwyntiau mewnol. Mewn geiriau eraill, maent yn onglau sydd ochr yn ochr, neu'n gyfagos, yn rhannu "braich". Mae onglau cyfagos sy'n cyfateb i ongl sgwâr, ongl syth, neu ongl lawn yn arbennig ac fe'u gelwir yn onglau cyflenwol, atodol ac esboniadol yn y drefn honno.
Cyfuno parau o onglau[golygu | golygu cod]
Mae tri phâr ongl arbennig yn cynnwys crynhoi onglau:

- Mae onglau cyflenwol yn barau o ongl y mae eu mesurau'n cyfateb i un ongl sgwâr (1/4 tro, 90 °, neu radian).[10] Os yw'r ddwy ongl gyflenwol yn gyfagos, mae eu hochrau nad ydynt yn cael eu rhannu yn ffurfio ongl sgwâr. Mewn geometreg Ewclidaidd, mae'r ddwy ongl lem mewn triongl dde yn gyflenwol (complementary), oherwydd bod swm onglau mewnol triongl yn 180 gradd, ac mae'r ongl sgwâr ei hun yn cyfrif am 90 gradd.
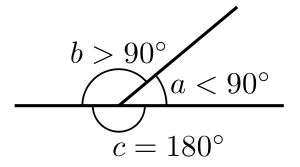
- Dwy ongl sy'n cyfateb i ongl syth (1/2 tro, 180°, neu radianau π) yn cael eu galw'n onglau atodol. [11]
- Mae dwy ongl sy'n creu ongl gyflawn (1 tro llawn, 360°, neu 2π radian) yn cael eu galw'n onglau explementary neu onglau cyfun.
- Gelwir y gwahaniaeth rhwng ongl ac ongl gyflawn yn esboniad o'r ongl neu gyfuniad yr ongl.
Onglau sy'n gysylltiedig â pholygon[golygu | golygu cod]
- Gelwir ongl sy'n rhan o bolygon syml yn ongl fewnol os yw'n gorwedd y tu mewn i'r polygon syml hwnnw. Mae gan bolygon ceugrwm syml o leiaf un ongl fewnol sy'n ongl atgyrch.
- Mewn geometreg Ewclidaidd, mae mesurau onglau mewnol triongl yn adio i π radian, 180 °, neu 1/2 tro; mae mesurau onglau mewnol syml amgrwm pedrochr yn ychwanegu hyd at 2π radian, 360°, neu 1 tro.
- Gelwir ychwanegiad ongl fewnol yn ongl allanol, hynny yw, mae ongl fewnol ac ongl allanol yn ffurfio pâr llinol o onglau . Mae dwy ongl allanol ym mhob fertig y polygon, pob un wedi'i bennu trwy ymestyn un o ddwy ochr y polygon sy'n cwrdd wrth y fertig; mae'r ddwy ongl hyn yn fertigol ac felly maent yn gyfartal. Mae ongl allanol yn mesur faint o gylchdro y mae'n rhaid ei wneud mewn fertig i olrhain (trace) y polygon.[12]
Mesur onglau[golygu | golygu cod]
Mae maint ongl geometrig fel arfer yn cael ei nodweddu gan faint y cylchdro lleiaf sy'n mapio un o'r pelydrau (neu linellau) i'r llall. Dywedir bod onglau sydd â'r un maint yn gyfartal neu'n gyfath neu'n gyfartal o ran mesur .
Unedau[golygu | golygu cod]
Trwy gydol hanes, mae onglau wedi'u mesur mewn llawer o wahanol unedau. Gelwir y rhain yn unedau onglog, a'r unedau mwyaf cyfoes yw gradd ( ° ), y radian (rad), a'r graddian (gradd), er bod llawer o rai eraill wedi'u defnyddio trwy gydol hanes.[13]
Diffinnir mwyafrif yr unedau mesur onglog fel bod un tro (hy un cylch llawn) yn hafal i n uned, ar gyfer rhai rhif cyfan n. Y ddau eithriad yw'r radian a'r rhan diamedr.
Onglau rhwng cromliniau[golygu | golygu cod]

Diffinnir yr ongl rhwng llinell a chromlin (ongl gymysg) neu rhwng dwy gromlin croestoriadol (ongl gromliniol) yw'r ongl rhwng y tangiadau ar bwynt y croestoriad. Mae enwau amrywiol (anaml bellach, os bu erioed, yn cael eu defnyddio) wedi'u rhoi i achosion penodol.[5]
Cyfeiriadau[golygu | golygu cod]
- ↑ Sidorov 2001
- ↑ Sidorov, L.A. (2001), "Angle", yn Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- ↑ (Saesneg) Joyce, David E. (2006). Angle measurement. Prifysgol Clark. Adalwyd ar 31 Hydref 2012.
- ↑ Slocum 2007
- ↑ 5.0 5.1 Chisholm 1911; Heiberg 1908
- ↑ "Mathwords: Reference Angle". www.mathwords.com. Archifwyd o'r gwreiddiol ar 23 Hydref 2017. Cyrchwyd 26 April 2018.
- ↑ Wong & Wong 2009, tt. 161–163
- ↑ Euclid (1753). The Elements. Proposition I:13.
- ↑ 9.0 9.1 Shute, Shirk & Porter 1960.
- ↑ "Complementary Angles". www.mathsisfun.com. Cyrchwyd 2020-08-17.
- ↑ "Supplementary Angles". www.mathsisfun.com. Cyrchwyd 2020-08-17.
- ↑ Henderson & Taimina 2005, t. 104.
- ↑ "angular unit". TheFreeDictionary.com. Cyrchwyd 2020-08-31.

