Hafaliad
Carreg glo pob hafaliad yw'r arwydd =, ac fe'i defnyddiwyd am y tro cyntaf gan y Cymro Robert Recorde yn yr hafaliad yma, sy'n mynegi 14x + 15 = 71, yn ein nodiant ni heddiw. Allan o'i gyfrol The Whetstone of Witte (1557). | |
| Math | fformiwla |
|---|---|
| Y gwrthwyneb | inequation |
| Yn cynnwys | hafalnod |
Gosodiad mathemategol yw hafaliad (Saesneg: equation), sy'n cynnwys un neu ragor o newidynnau. Mae'n ddull o fynegi fod dau wrthrych mathemategol (rhifau, fel arfer) yn union yr un peth. Mynegir hyn yn symbolaidd â'r hafalnod, = , a ddefnyddiwyd yn gyntaf gan y mathemategwr o Gymro, Robert Recorde (tua 1510 – 1558). Dyma rai enghreifftiau o hafaliadau:
- 2 + 3 = 5, neu
- x − x = 0, neu
- x = y , neu
- x + 1 = 2.
Unfathiannau yw'r cyntaf a'r ail: maent yn wir, pa bynnag werth a gymer y newidynnau ynddynt. Lle nad yw hafaliad yn unfathiant, fe all y gosodiad fod yn wir neu'n anwir yn dibynnu ar werthoedd y newidynnau ynddo. Fe gelwir gwerthoedd o'r newidynnau sy'n peri i'r gosodiad fod yn wir yn wreiddiau (neu datrysiadau) yr hafaliad. Dywedir eu bod yn bodlonni yr hafaliad. Yn y drydedd enghraifft uchod, mae nifer anfeidrol o ddatrysiadau, x = 1 , y = 1 er enghraifft. Yn y bedwaredd enghraifft, dim ond un datrysiad, x = 1 sy'n bodoli. Dywedir ei fod yn wraidd unigryw.
Priodweddau elfennol[golygu | golygu cod]
Mewn algebra elfenol, os yw hafaliad yn wir, fe ellir deillio hafaliad gwir arall ohono wrth wneud y canlynol:
- Adio rhif i ddwy ochr yr hafaliad.
- Tynnu rhif o ddwy ochr yr hafaliad.
- Lluosi dwy ochr yr hafaliad â'r un rhif.
- Rhannu dwy ochr yr hafaliad ag unrhyw rhif an-sero.
- Yn gyffredinol, gellir gymhwyso ffwythiant i'r ddwy ochr.
Mae hafaledd yn enghraifft o berthynas unfathiant.
Mae datrys hafaliad sy'n cynnwys newidynnau yn cynnwys penderfynu pa werthoedd o'r newidynnau sy'n gwneud y cydraddoldeb yn gywir. Gelwir y newidynnau y mae'n rhaid datrys yr hafaliad ar eu cyfer hefyd yn anhysbysion (unknowns), a gelwir gwerthoedd yr anhysbysion sy'n bodloni'r cydraddoldeb yn ddatrysiadau yr hafaliad. Mae dau fath o hafaliad: unfathiant (identities) a hafaliadau amodol. Mae unfathiant yn wir am holl werthoedd y newidynnau; mae hafaliad amodol, ar y llaw arall, yn wir am werthoedd penodol y newidynnau yn unig.[1]
Ysgrifennir hafaliad fel dau ymadrodd, wedi'u cysylltu gan hafalnod ("="), symbol a ddyfeiswyd yn 1557 gan y Cymro Robert Recorde.[2] Gelwir yr ymadroddion ar ddwy ochr yr hafalnod yn "ochr chwith" ac "ochr dde" yr hafaliad. Yn aml iawn tybir bod ochr dde hafaliad yn sero. Gan dybio nad yw hyn yn lleihau'r cyffredinolrwydd, oherwydd gellir gwireddu hyn trwy dynnu'r ochr dde o'r ddwy ochr.
Y math mwyaf cyffredin o hafaliad yw hafaliad polynomial (a elwir yn gyffredin hefyd yn hafaliad algebraidd) lle mae'r ddwy ochr yn polynomialau. Mae ochrau hafaliad polynomial yn cynnwys un neu fwy o dermau. Er enghraifft, yr hafaliad
mae ganddo ochr chwith , sydd â phedwar 'term' ac ochr dde , sy'n cynnwys un term yn unig. Mae enwau'r newidynnau yn awgrymu bod x ac y yn anhysbys, a bod A, B, ac C yn baramedrau, ond fel arfer mae hyn yn cael ei bennu gan y cyd-destun.
Mae hafaliad yn cyfateb i glorian, lle rhoddir pwysau arni. Pan roddir pwysau cyfartal o rywbeth (ee grawn) yn y ddwy badell, mae'r ddau bwysau yn achosi i'r raddfa fod mewn 'cydbwysedd' a dywedir eu bod yn gyfartal. Os tynnir swm o rawn o un badell o'r glorian, yna mae'n rhaid tynnu swm cyfartal o rawn o'r badell arall i gadw cydbwysedd. Yn fwy cyffredinol, mae hafaliad yn parhau i fod mewn cydbwysedd os cyflawnir yr un gweithrediad ar y ddwy ochr.
Mewn geometreg Cartesaidd (neu 'ddadansoddol'), defnyddir hafaliadau i ddisgrifio ffigurau geometrig. Gan fod gan yr hafaliadau sy'n cael eu hystyried, fel hafaliadau ymhlyg (Implicit function) neu hafaliadau parametrig, lawer o atebion, mae'r amcan bellach yn wahanol: yn lle rhoi'r atebion yn benodol neu eu cyfrif, sy'n amhosibl, defnyddir yr hafaliadau i astudio priodweddau ffigurau. Dyma'r syniad cychwynnol yr hyn a elwir yn geometreg algebraidd, maes pwysig o fathemateg.
Mae Algebra'n astudio dau brif deulu o hafaliadau: hafaliadau polynomial a hafaliadau llinol. Pan nad oes ond un newidyn, mae gan hafaliadau polynomial y ffurf P(x) = 0, lle mae P yn polynomial, ac mae gan hafaliadau llinol y ffurf ax + b = 0, lle mae a a b yn baramedrau. I ddatrys hafaliadau gan y naill deulu neu'r llall, defnyddir technegau algorithmig neu geometrig sy'n tarddu o algebra llinol neu ddadansoddiad mathemategol. Mae Algebra hefyd yn astudiaeth o hafaliadau Diophantine lle mae'r cyfernodau a'r datrusiadau yn gyfanrifau. Mae'r technegau a ddefnyddir yn wahanol ac yn dod o theori rhif. Mae'r hafaliadau hyn yn anodd yn gyffredinol; mae person yn aml yn chwilio dim ond i ddarganfod bodolaeth neu absenoldeb datrysiad, ac, os ydynt yn bodoli, i gyfrif nifer yr atebion.
Mae hafaliadau differol (neu 'wahaniaethol') yn hafaliadau sy'n cynnwys un neu fwy o swyddogaethau a'u deilliadau. Fe'u datrysir trwy ddod o hyd i fynegiad ar gyfer y ffwythiant nad yw'n cynnwys deilliadau. Defnyddir hafaliadau gwahaniaethol i fodelu prosesau sy'n cynnwys cyfraddau newid y newidyn, ac fe'u defnyddir mewn meysydd fel ffiseg, cemeg, bioleg ac economeg.
Cyflwyniad[golygu | golygu cod]
Darlun analog[golygu | golygu cod]

Mae hafaliad yn cyfateb i glorian neu si-so.
Yn y llun, mae x, y a z i gyd yn feintiau gwahanol (yn yr achos hwn rhifau real ) a gynrychiolir fel pwysau crwn, ac mae pwysau gwahanol ar bob un o x, y , a z. Mae adio yn cyfateb i ychwanegu pwysau, tra bod tynnu yn cyfateb i dynnu pwysau o'r hyn sydd yno eisoes. Pan fydd cydraddoldeb, mae cyfanswm y pwysau ar bob ochr yr un peth.
Paramedrau ac anhysbysion[golygu | golygu cod]
Mae hafaliadau yn aml yn cynnwys termau heblaw'r anhysbysion. Fel rheol, gelwir y termau eraill hyn, y tybir eu bod yn hysbys yn gysonion, cyfernodau neu baramedrau.
Enghraifft o hafaliad sy'n cynnwys x ac y fel anhysbysion a'r paramedr R yw
Pan ddewisir R i fod â gwerth 2 ( R = 2), byddai'r hafaliad hwn yn cael ei gydnabod mewn cyfesurynnau Cartesaidd fel yr hafaliad ar gyfer y cylch radiws o 2 o amgylch y tardd. Felly, yr hafaliad gydag R amhenodol yw'r hafaliad cyffredinol ar gyfer y cylch.
Fel arfer, dynodir yr anhysbysion gan lythrennau ar ddiwedd yr wyddor, x, y, z, w, ..., tra bod cyfernodau (paramedrau) yn cael eu dynodi gan lythrennau ar ddechrau'r wyddor, a, b, c, d,. . . . Er enghraifft, yr hafaliad cwadratig cyffredinol fel arfer yw ax2 + bx + c = 0.
Gelwir y broses o ddod o hyd i'r atebion, neu, yn achos y paramedrau, mynegi'r anhysbys yn nhermau'r paramedrau, yn 'ddatrys yr hafaliad'. Gelwir mynegiadau o'r fath o'r atebion o ran y paramedrau hefyd yn atebion.
Mae system o hafaliadau yn set o hafaliadau cydamserol (simultaneous equations), fel arfer mewn sawl anhysbys y ceisir yr atebion cyffredin ar eu cyfer. Felly, mae'r ateb i'r system yn set o werthoedd ar gyfer pob un o'r anhysbysion, sydd gyda'i gilydd yn ffurfio ateb i bob hafaliad yn y system. Er enghraifft, mae gan y system
y datrysiad unigryw x = −1, y = 1.
Unfathiant[golygu | golygu cod]
Mewn mathemateg unfathiant (Saesneg: identity) yw perthynas yr hafaledd A = B, fel bod A a B yn cynnwys rhai newidynnau a lle mae A a B yn rhoi'r un gwerthoedd a'i gilydd, ni waeth be fo'r gwerthoedd (rhifau, fel arfer) a gaiff eu cyfnewid am newidynnau. Mewn geiriau eraill, mae A = B yn unfathiant os yw A a B yn diffinio yr un ffwythiannau. Golyga hyn fod yr 'unfathiant' yn 'hafaledd' (equality) rhwng ffwythiannau a ddiffiniwyd yn wahanol. Er enghraifft, mae (a + b)2 = a2 + 2ab + b2 a cos2(x) + sin2(x) = 1 yn unfathiannau.
Caiff unfathiannau eu dynodi gan y symbol ≡ (bariau triphlyg ), yn hytrach na =, sef yr hafaliad.[3]
Mewn geiriau eraill: enghraifft o unfathiant yw'r gwahaniaeth rhwng dau sgwâr:
sy'n wir am bob x ac y.
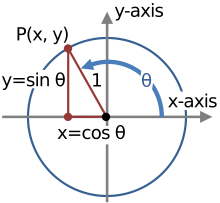
Mae trigonometreg yn faes lle mae llawer o unfathianau'n bodoli; mae'r rhain yn ddefnyddiol wrth drin neu ddatrys hafaliadau trigonometrig. Dau o lawer sy'n cynnwys y swyddogaethau sin a chosin yw:
lle mae θ wedi'i gyfyngu i rhwng 0 a 45 gradd, gall un ddefnyddio'r hunaniaeth uchod i'r cynnyrch roi:
sydd ill dau'n wir am holl werthoedd θ.
Er enghraifft, i ddatrys gwerth θ sy'n bodloni'r hafaliad:
sy'n ildio'r datrysiad canlynol ar gyfer θ:
Priodweddau[golygu | golygu cod]
Mae dwy hafaliad neu ddwy system o hafaliadau yn gyfwerth, os oes ganddyn nhw'r un set o atebion. Mae'r gweithrediadau canlynol yn trawsnewid hafaliad neu system o hafaliadau yn un gyfwerth - ar yr amod bod y gweithrediadau yn ystyrlon ar gyfer yr ymadroddion y maent yn berthnasol iddynt:
- Adio neu dynnu'r un maint i (neu o) ddwy ochr hafaliad. Mae hyn yn dangos bod pob hafaliad yn cyfateb i hafaliad lle mae'r ochr dde yn sero.
- Lluosi neu rannu dwy ochr hafaliad â maint nad yw'n sero.
- Cymhwyso unfathiant i drawsnewid un ochr i'r hafaliad. Er enghraifft, ehangu lluoswm neu ffactoreiddio swm.
- Ar gyfer system: ychwanegu ochr gyfatebol hafaliad arall i ddwy ochr hafaliad, wedi'i luosi â'r un maint.
Er enghraifft, mae
Algebra[golygu | golygu cod]
Hafaliadau polynomial[golygu | golygu cod]

Yn gyffredinol, hafaliad algebraidd neu hafaliad polynomial yw hafaliad o'r ffurf
- , neu
lle mae P a Q yn polynomialau â chyfernodau mewn rhai maes (ee rhifau rhesymegol, rhifau real, rhifau cymhlyg). Mae hafaliad algebraidd yn un-amrywedd (univariate) os yw'n cynnwys un newidyn yn unig. Ar y llaw arall, gall hafaliad polynomial gynnwys sawl newidyn, ac os felly fe'i gelwir yn aml-amrywedd (multivariate; newidynnau lluosog, x, y, z, ac ati). Mae'r term hafaliad polynomial fel arfer yn cael ei ddefnyddio'n hytrach nag hafaliad algebraidd.
Mae system hafaliadau llinol (neu system linellol) yn gasgliad o hafaliadau llinol sy'n cynnwys yr un set o newidynnau. [b] Er enghraifft, mae
yn hafaliad algebraidd (polynomial) yn univariate gyda chyfernodau cyfanrif a
yn hafaliad polynomial aml-amrywedd dros y rhifau rhesymegol.
Systemau hafaliadau llinol[golygu | golygu cod]

yn system o dri hafaliad yn y tri newidyn x, y, z . Datrysiad i system linellol yw aseiniad rhifau i'r newidynnau fel bod yr holl hafaliadau'n cael eu bodloni ar yr un pryd. Rhoddir datrysiad i'r system uchod gan
gan ei fod yn gwneud y tri hafaliad yn ddilys. Mae'r gair "system" yn nodi bod yr hafaliadau i'w hystyried ar y cyd, yn hytrach nag yn unigol.
Mewn mathemateg, theori systemau llinol yw sylfaen a rhan sylfaenol algebra llinol, pwnc a ddefnyddir yn y rhan fwyaf o fathemateg fodern. Mae algorithmau cyfrifiadol ar gyfer dod o hyd i'r atebion yn rhan bwysig o algebra llinol rhifiadol, ac maent yn chwarae rhan amlwg mewn ffiseg, peirianneg, cemeg, gwyddoniaeth gyfrifiadurol, ac economeg. Gellir brasamcanu system o hafaliadau aflinol yn aml drwy system llinol, techneg ddefnyddiol wrth wneud model mathemategol neu efelychiad cyfrifiadurol o system gymharol gymhlyg.
Geometreg[golygu | golygu cod]
Geometreg ddadansoddol[golygu | golygu cod]

Mewn geometreg Ewclidaidd, mae'n bosibl cysylltu set o gyfesurynnau â phob pwynt yn y gofod, er enghraifft gan grid orthogonal. Mae'r dull hwn yn caniatáu i un nodweddu ffigurau geometrig drwy hafaliadau. Gellir mynegi plân mewn gofod tri dimensiwn fel set i ateb hafaliad y ffurf , lle mae a yn rhifau real a yw'r pethau anhysbys sy'n cyfateb i gyfesurynnau pwynt yn y system a roddir gan y grid orthogonal. Y gwerthoedd yw cyfesurynnau fector sy'n berpendicwlar i'r plân a ddiffinnir gan yr hafaliad. Gall llinell gael ei mynegi fel croestoriad dwy blân, hynny yw fel set sy'n ateb yr hafaliad llinol sengl gyda gwerthoedd yn neu fel set datrysiad dau hafaliad llinol â gwerthoedd yn
Adran conig yw croestoriad côn ag hafaliad a phlân. Mewn geiriau eraill, yn y gofod, diffinnir pob conig fel set datrysiad hafaliad plân a hafaliad côn. Mae'r ffurfioldeb hwn yn caniatáu i un bennu lleoliad a phriodweddau ffocysau conig.
Hafaliadau Cartesaidd[golygu | golygu cod]
Mae system gyfesurynnol Gartesaidd yn system system o gyfesurynnau sy'n pennu pob pwynt unigryw mewn plân gan bâr o gyfesurynnau rhifiadol, sef y pellteroedd o'r pwynt i ddwy linell sefydlog berpendicwlar, sy'n cael eu marcio gan ddefnyddio'r un uned o hyd.
Damcaniaeth rhif[golygu | golygu cod]
Hafaliadau Diophantine[golygu | golygu cod]
Mae hafaliad Diophantine yn hafaliad polynomial mewn dau anhysbys neu fwy - lle ceisir dim ond datrysiad cyfanrif (integer solution) ar eu cyfer; mae datrysiad cyfanrif yn ddatrysiad fel bod yr holl bethau anhysbys yn cymryd gwerthoedd cyfanrif). Mae hafaliad Diophantine llinol yn hafaliad rhwng dau swm o fonomial o radd sero neu un. Enghraifft o hafaliad Diophantine llinol yw lle mae a, b, ac c yn gysonion. Mae hafaliad Diophantine esbonyddol yn un y gall esbonwyr termau'r hafaliad fod yn anhysbys ar ei gyfer.
Mae gan broblemau diophantine lai o hafaliadau na newidynnau anhysbys ac maent yn cynnwys dod o hyd i gyfanrifau sy'n gweithio'n gywir ar gyfer pob hafaliad. Mewn iaith fwy technegol, maent yn diffinio cromlin algebraidd, arwyneb algebraidd, neu wrthrych mwy cyffredinol, ac yn gofyn am y pwyntiau dellt (lattice points) arno.
Mae'r gair Diophantine yn cyfeirio at fathemategydd Helenistig y 3g, sef Diophantus o Alexandria, a wnaeth astudiaeth o hafaliadau o'r fath ac a oedd yn un o'r mathemategwyr cyntaf i gyflwyno symbolaeth i algebra. Bellach gelwir yr astudiaeth fathemategol o broblemau Diophantine a gychwynnodd Diophantus yn 'ddadansoddiad Diophantine'.
Hafaliadau differol[golygu | golygu cod]

Hafaliad differol yw hafaliad mathemategol sy'n cysylltu rhywfaint o ffwythiant â'i ddeilliannau. Mewn cymwysiadau, mae'r ffwythiannau fel arfer yn cynrychioli meintiau corfforol, mae'r deilliadau'n cynrychioli eu cyfraddau newid, ac mae'r hafaliad yn diffinio perthynas rhwng y ddau. Oherwydd bod cysylltiadau o'r fath yn hynod gyffredin, mae hafaliadau differol yn chwarae rhan amlwg mewn llawer o ddisgyblaethau gan gynnwys ffiseg, peirianneg, economeg a bioleg.
Geometreg algebraidd[golygu | golygu cod]
Mae geometreg algebraidd yn astudiaeth o seroau ('isradd' neu 'sero'r ffwythiant') polynomialau aml-gyfeiriol. Mae geometreg algebraidd modern yn seiliedig ar y defnydd o dechnegau algebra haniaethol, yn bennaf ar gyfer datrys problemau geometrig am setiau o seros. Amcanion sylfaenol yr astudiaeth o geometreg algebraidd yw 'amrywiaeth algebraidd'. Amrywiaeth algebraidd, felly, yw prif faes astudiaeth geometreg algebraidd.
Ymhlith yr amrywiaeth algebraidd a astudir fwyaf aml mae comliniau algebraidd sy'n cynnwys llinellau, cylchoedd, elipsau, hyperbolâu, llinellau, parabolâu, cromlinau ciwbic a chromlinau cwartig. Mae geometreg algebraidd yn cymryd lle canolog mewn mathemateg fodern ac mae ganddo lawer o gysylltiadau cysyniadol a meysydd mor amrywiol â dadansoddiad cymhleth, topoleg a theori rhif.
Mathau o hafaliadau[golygu | golygu cod]
Gellir dosbarthu hafaliadau yn ôl y mathau o weithrediadau a meintiau dan sylw. Ymhlith y mathau pwysig mae:
- hafaliad algebraidd neu hafaliad polynomial, lle mae'r ddwy ochr yn polynomialau (gweler hefyd system hafaliadau polynomial). Dosberthir y rhain ymhellach yn ôl gradd :
- hafaliad llinol argyfer gradd un
- hafaliad cwadratig ar gyfer gradd dau
- hafaliad ciwbig ar gyfer gradd tri
- hafaliad cwartig ar gyfer gradd pedwar
- hafaliad quintig ar gyfer gradd pump
- hafaliad sextig ar gyfer gradd chwech
- hafaliad septig ar gyfer gradd saith
- hafaliad octig ar gyfer gradd wyth
- hafaliad Diophantine lle mae'n ofynnol i'r anhysbys fod yn gyfanrifau
- hafaliad trosgynnol, sy'n cynnwys swyddogaeth drosgynnol ei anhysbys
- hafaliad parametrig, lle mae'r datrysiadau ar gyfer y newidynnau yn cael eu mynegi fel swyddogaethau rhai newidynnau eraill, o'r enw paramedrau sy'n ymddangos yn yr hafaliadau
- hafaliad swyddogaethol, lle mae'r anhysbys yn ffwythiant yn hytrach na meintiau syml
- hafaliadau sy'n cynnwys deilliadau, integrynnau a gwahaniaethau meidraidd ee:
- hafaliad differol
- hafaliad cyfannol (neu 'Integral equation')
- hafaliad swyddogaethol
- hafaliad integro-differential
Cyfeiriadau[golygu | golygu cod]
- ↑ Lachaud, Gilles. "Équation, mathématique". Encyclopædia Universalis (yn Ffrangeg).
- ↑ "Equation - Math Open Reference". www.mathopenref.com. Cyrchwyd 2020-09-01.
- ↑ Weiner, Joan (2004).Frege Explained. Open Court.
Dolenni allanol[golygu | golygu cod]
- Winplot : Cynllwynwr Pwrpas Cyffredinol sy'n gallu darlunio ac animeiddio hafaliadau mathemategol 2D a 3D.
- Cynllwynwr hafaliad : Mae tudalen we ar gyfer cynhyrchu a lawrlwytho plotiau pdf neu ôl-nodyn o'r datrysiad yn gosod hafaliadau ac anghydraddoldebau mewn dau newidyn ( x ac y ).
Gwall cyfeirio: Mae tagiau <ref> yn bodoli am grŵp o'r enw "lower-alpha", ond ni ellir canfod y tag <references group="lower-alpha"/>
























