Gofod tri dimensiwn
 | |
| Math | space in mathematics, gwrthrych 3-dimensiwn |
|---|---|
| Rhan o | Gofod pedwar dimensiwn |
| Rhagflaenwyd gan | gofod dau ddimensiwn |
| Olynwyd gan | Gofod pedwar dimensiwn |



Mewn Mathemateg, mae gofod tri dimensiwn ('gofod-3', neu 'gofod 3-ddimensiwn') yn lleoliad geometrig lle nodir safle rhyw elfen (e.e. pwynt neu groesbwynt) gan dri gwerth a elwir yn "baramedrau"; dyma'r diffiniad anffurfiol.
Caiff ei gynrychioli'n gyffredin gan y symbol ℝ3.
Mewn ffiseg a mathemateg, gellir deall dilyniant o rifau a elwir yn n fel lleoliad mewn gofod n-ddimensiwn. Pan fo n = 3, gelwir y set o bob lleoliad o'r un fath yn "ofod Ewclidaidd tri dimensiwn". Mae hyn yn gweithredu fel model tri pharamedr o'r bydysawd ffisegol (hynny yw, y rhan ofodol, heb ystyried amser) lle mae pob mater sy'n hysbys yn bodoli. Ond, un enghraifft yn unig yw hwn o nifer helaeth o ofodau mewn tri dimensiwn a elwir yn "3-maniffold". Yma, pan fo tri gwerth yn cyfeirio at fesuriadau gwahanol, mewn cyfeiriadau gwahanol (h.y. cyfesurynnau), yna gellir dewis unrhyw un o'r tri chyfeiriad, cyn belled nad yw'r fectorau yn y cyfeiriadau hyn yn gorwedd yn y plân 2-ofod. Ymhellach, yn yr achos yma, gall y tri gwerth yma gael eu labelu gan unrhyw gyfuniad o'r tri term: lled, hyd ac uchder.
Geometreg Ewclidaidd
[golygu | golygu cod]- Prif: Geometreg Ewclidaidd
Y system gyfesurynnol
[golygu | golygu cod]- Prif: System cyfesurynnau
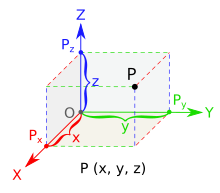
Mewn mathemateg, mae geometreg ddadansoddol (a elwir hefyd yn "geometreg Cartesaidd") yn disgrifio pob pwynt mewn gofod tri dimensiwn trwy dri chyfesuryn. Rhoddir tair echelin gyfesurynnol, gyda phob un yn berpendicwlar i'r ddau arall ar y tarddiad, sef y pwynt lle y maent yn croesi. Fe'u labelir fel arfer yn x, y, a z. O ran yr echeliniau hyn, mae lleoliad unrhyw bwynt o fewn y gofod tri dimensiwn yn cael ei roi gan driawd trefnedig (ordered triple) o rifau real, gyda phob rhif sy'n rhoi pellter y pwynt hwnnw o'r tarddiad, wedi'i fesur ar hyd yr echelin a roddir, sy'n hafal i bellter y pwynt hwnnw o'r plân a bennir gan y ddau echelin arall.[1]
Ceir dulliau poblogaidd eraill o ddisgrifio lleoliad pwynt mewn gofod tri dimensiwn, gan gynnwys 'cydlynu silindraidd' a 'chyfesurynnau sfferig]]; mewn gwirionedd, ceir nifer diddiwedd o ddulliau posibl.
Llinellau a planau
[golygu | golygu cod]Mae dau bwynt gwahanol bob amser yn pennu llinell (syth). Mae tri phwynt gwahanol naill ai'n gyflinellol (collinear) neu'n pennu y plân unigryw. Gall pedwar pwynt gwahanol fod naill ai'n gyflinellol, yn gymhlan (coplanar) neu'n pennu ar y gofod cyfan.
Sfferau a pheli
[golygu | golygu cod]
Mae sffêr mewn gofod-3 (a elwir hefyd yn "2-sffêr" oherwydd ei fod yn wrthrych 2-ddimensiwn) yn cynnwys y set o bob pwynt mewn gofod-3 ar bellter sefydlog r o bwynt canolog P. Gelwir y solet a amgylchynir gan y sffer yn "bêl" (neu, i fod yn fanwl gywir, yn "3-pêl"). Rhoddir cyfaint y bêl gan
- .
Mae math arall o sffêr (sy'n codi o 4-pêl ac sydd ag arwynebedd tri dimeensiwn) yw'r 3-sffêr, a'i bwyntiau sy'n gytbell o dardd y gofod Ewclidaidd ℝ4. Os oes cyfesurynnau P(x, y, z, w) gan bwynt yna mae x2 + y2 + z2 + w2 = 1 yn nodweddu'r pwyntiau hynny ar y sfer-3, wedi'i ganoli ar ei dardd.[2]
Polytopau
[golygu | golygu cod]Mewn tri dimensiwn, ceir naw naw polytop rheolaidd: y 5 amgrwm a'r 4 nad ydynt yn amgrwm (sef y polytopau Kepler-Poinsot).
| Class | Solidau platonig | Polyhedra Kepler-Poinsot | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Cymesuredd | Td | Oh | Ih | ||||||
| Grŵp Coxeter | A3, [3,3] | B3, [4,3] | H3, [5,3] | ||||||
| Trefn | 24 | 48 | 120 | ||||||
| Polyhedron Rheolaidd |
{3,3} |
 {4,3} |
 {3,4} |
 {5,3} |
{3,5} |
 {5/2,5} |
 {5,5/2} |
{5/2,3} |
 {3,5/2} |
Cyfeiriadau
[golygu | golygu cod]- ↑ Hughes-Hallett, Deborah; McCallum, William G.; Gleason, Andrew M. (2013). Calculus : Single and Multivariable (arg. 6). John wiley. ISBN 978-0470-88861-2.
- ↑ Brannan, Esplen & Gray 1999, tt. 34–5

