Teseract
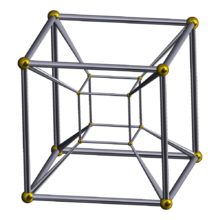
Analog pedwar-dimensiwn o'r ciwb yw teseract o fewn maes geometreg. Mae'r teseract i'r ciwb, yr hyn yw'r ciwb i'r sgwâr. Yn union fel y mae gan arwyneb y ciwb chwe ochr sgwâr, mae uwcharwynebau'r teseract yn cynnwys wyth cell ciwbig. Mae'r tesseract, hefyd, yn un o'r chwech polytop-4 rheolaidd amgrwm.
Gelwir y teseract hefyd wrth yr enwau canlynol: wyth-cell, C8, octachoron (rheolaidd), octahedroid,[1] prism ciwbig a tetraciwb.[2] Hwn yw'r hyperciwb 4-dimensiwn o fewn y teulu o hyperciwbiau.[3]
Yn ôl yr Oxford English Dictionary, bathwyd y gair teseract yn 1888 gan Charles Howard Hinton yn ei lyfr A New Era of Thought, ac mae'r gair yn air cyfansawdd o'r Groeg τέσσερεις ακτίνες (téssereis aktines, "pedwar pelydryn"), sy'n cyfeirio at y bedair linell a ddaw o bob fertig.[4] Y sillafiad gwreiddiol oedd "tessaract".
Geometreg
[golygu | golygu cod]Gellir llunio teseract mewn sawl ffordd. Fel polytop rheolaidd gyda thri ciwb wedi'i plygu i'w gilydd o gwmpas pob ymyl, mae ganddo symbol Schläfli {4,3,3} a chyfesuredd hyperoctahedral yn nhrefn 384. O'i lunio fel hyperprism 4D a wnaed o ddau giwp paralel (cyfochrog), gellir ei enwi fel y symbol Schläfli cyfansawdd {4,3} × { }, gyda threfn cymesuredd o 96. Fel deubrism 4-4, a lluoswm Cartesaidd o ddau sgwâr, gellir ei enwi gyda symbol Schläfli cyfansawdd {4}×{4}, gyda threfn cymesuredd o 64. Fel orthotop, caiff ei ddynodi gan y symbol Schläfli cyfansawdd { } × { } × { } × { } neu { }4, gyda threfn cymesuredd o 16.
Gan fod pob fertig o'r teseract gyferbyn a 4 ymyl, mae ffigwr fertig o'r teseract yn tetrahedron rheolaidd. Gelwir y polytop deuol o'r teseract yn "hecsadecachoron rheolaidd", neu 16-cell, gyda'r symbol Schläfli o {3,3,4}.
O fewn gofod pedwar dimensiwn Euclidaidd, nodir y teseract arferol mewn dull crynno-amgrwm (convex hull) o'r pwyntiau (±1, ±1, ±1, ±1). H.y. mae'n cynnwys y pwyntiau:
Taflunio i ddau ddimensiwn
[golygu | golygu cod]Gellir dychmygu llunio hyperciwb fel hyn:
- 1-dimensiwn: Gellir cysylltu llinell o ddau bwynt A a B, sy'n rhoi llinell segment newydd AB.
- 2-ddimensiwn: Gellir cysylltu dwy linell segment cyfochrog (paralel) AB a CD i greu sgwâr ABCD.
- 3-dimensiwn: Gellir cysylltu dau sgwâr paralel ABCD a EFGH i greu ciwb, ABCDEFGH.
- 4-dimensiwn: Gellir cysylltu dau giwb paralel ABCDEFGH a IJKLMNOPi greu hyperciwb, gyda'r corneli wedi eu nodi fel ABCDEFGHIJKLMNOP.

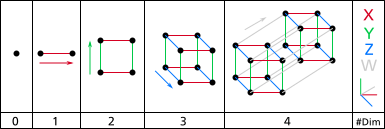 |
 |
Mae'n bosibl taflunio terseractau i mewn i ofod tri- a dau—dimensiwn, fel y gellir taflunio ciwb i ofod dau-ddimensiwn.
Cyfeiriadau
[golygu | golygu cod]- ↑ Matila Ghyka, The geometry of Art and Life (1977), tud.68
- ↑ Gall y term yma (tetraciwb) hefyd gyfeirio at y polyciwb, sy'n cynnwys pedwar ciwb.
- ↑ E. L. Elte, The Semiregular Polytopes of the Hyperspaces, (1912)
- ↑ "Home : Oxford English Dictionary". Oed.com. Archifwyd o'r gwreiddiol ar 2018-01-22. Cyrchwyd 21 Ionawr 2018.

