Seiffr Caesar

Oddi ar Wicipedia
Mae seiffr Caesar yn disodli pob llythyren y destun-plaen gydag un gwahanol sydd nifer sefydlog o leoedd i lawr yr wyddor. Mae'r seiffr a ddangosir yma yn defnyddio shifft tri i'r chwith, fel bod (er enghraifft) pob llythyren E y destun-plaen yn dod yn B yn y destun-seiffr.

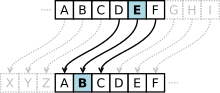
Mewn cryptograffeg, mae seiffr Caesar, a elwir hefyd y seiffr sifft, cod Caesar neu sifft Caesar, yn un o'r technegau amgryptio symlaf a mwyaf adnabyddus. Mae'n fath o seiffr amnewid lle caiff pob llythyren yn y destun-plaen ei ddisodli gan ryw lythyren unigryw arall, nifer sefydlog o safleoedd i lawr yr wyddor. Er enghraifft, gyda sifft o dri i'r chwith, bydd D cael ei ddisodli gan A, bydd E yn cael ei ddisodli gan B, ac yn y blaen. Enwir y dull ar ôl Julius Caesar, a ddefnyddiodd y seiffr hwn yn ei ohebiaeth breifat.[1]

Mae'r cam amgryptio a gyflawnir gan y seiffr Caesar yn aml yn cael ei defnyddio fel rhan o seiffrau mwy cymhleth, fel y seiffr Vigenère, ac mae'n dal i gael ei gymhwyso'n yn system ROT13 modern. Erbyn heddiw mae'n hawdd torri seiffr Caesar, ac felly'n anymarferol oherwydd nid yw'n cynnig unrhyw ddiogelwch cyfathrebu rhagor.

Enghraifft[golygu | golygu cod]

Gellir cynrychioli'r trawsnewidiad trwy alinio dwy wyddor; yr wyddor blaen a'r wyddor seiffr. Y wyddor seiffr yw'r wyddor blaen wedi'i sifftio i'r chwith neu'r dde gan ryw nifer o safleoedd. Er enghraifft, dyma seiffr Caesar sy'n defnyddio cylchdro dde o pum lle. Y paramedr sifft hwn yw allwedd y seiffr: 

Plaen:  A  B  C  Ch D  Dd E  F  Ff G  Ng H  I  J  L  Ll M  N  O  P  Ph R  Rh S  T  Th U  W  Y
Seiffr: Dd E  F  Ff G  Ng H  I  J  L  Ll M  N  O  P  Ph R  Rh S  T  Th U  W  Y  A  B  C  Ch D

Wrth amgryptio, mae angen edrych i fyny pob llythyren o'r neges yn y destun-blaen, ac yn ysgrifennu'r llythyren gyfatebol yn y destun-seiffr. 

Testun-plaen:  MAE HEN WLAD FY NHADAU YN ANNWYL I MI
Testun-seiffr: RDdH MHRh ChPDdG ID RhMDdGDdC DRh DdRhRhChDP N RN

Gallwn dad-seiffro'r neges trwy wneud y proses i'r cyfeiriad arall, gyda sifft o bump i'r chwith.

Gellir cynrychioli'r amgryptio hefyd gan ddefnyddio rhifyddeg fodiwlaidd (rhifyddeg cloc) trwy drawsnewid y llythrennau yn rhifau yn gyntaf, yn ôl y cynllun, A → 0, B → 1,. . ., Y → 28.[2] Gellir disgrifio amgryptio llythyren x gan shifft n yn fathemategol fel,[3]

Perfformir dadgryptio yn yr un modd,

(Mae yna ddiffiniadau gwahanol ar gyfer y gweithrediad modulo. Yn yr uchod, mae'r canlyniad yn yr amrediad 0 i 28; h.y., os nad yw x + n neu x − n o fewn yr amrediad 0 i 25, mae'n rhaid i ni dynnu neu ychwanegu 29.)

Gan fod yr amnewidiad yn aros yr un peth trwy gydol y neges, caiff y seiffr Caesar ei ddosbarthu fel math o amnewidiad monoalffabetig, yn hytrach nag amnewid polyalffabetig.

Hanes[golygu | golygu cod]

Enwir y seiffr Caesar ar ôl Julius Caesar, a ddefnyddiodd y dull.

Enwir y seiffr Caesar ar ôl Julius Caesar, a'i defnyddiodd, yn ôl Suetonius, gan ddefnyddio sifft o dri amddiffyn negeseuon o arwyddocâd milwrol. Er mai Caesar oedd y cyntaf a gofnodwyd ei defnydd, roedd seiffrau amnewid eraill yn hysbys yn gynharach.[4][5]

Dydyn ni ddim yn gwybod pa mor effeithiol oedd seiffr Caesar ar y pryd, ond mae'n debygol ei fod wedi bod yn weddol ddiogel, yn bennaf oherwydd byddai'r mwyafrif o elynion Caesar wedi bod yn anllythrennog, a byddai eraill wedi tybio bod y negeseuon wedi'u hysgrifennu mewn iaith dramor anhysbys.[6] Nid oes unrhyw gofnod ar y pryd o unrhyw dechnegau ar gyfer datrys seiffrau amnewid syml. Mae'r cofnodion cynharaf sydd wedi goroesi o dadseiffro seiffrau amnewid yn dyddio i waith Al-Kindi o'r 9fed ganrif yn y byd Arabaidd. Darganfuwyd dadansoddiad amledd.[7]

Yn y 19eg ganrif, byddai'r adran hysbysebion personol mewn papurau newydd weithiau'n cael ei defnyddio i gyfnewid negeseuon wedi'u hamgryptio gan ddefnyddio seiffrau syml. Mae enghreifftiau o gariadon yn anfon cyfathrebiadau cyfrinachol wedi'u hamgryptio gan seiffr Caesar yn hysbysebion yn The Times.[8] Hyd yn oed mor ddiweddar â 1915, roedd seiffr Caesar yn cael ei ddefnyddio: roedd byddin Rwsia yn ei defnyddio yn lle seiffrau mwy cymhleth a oedd yn rhy anodd i'w milwyr deall; ond roedd yn hawdd i gryptolegwyr Almaeneg ac o Awstria i ddadgryptio'u negeseuon.[9]

Mae seiffr Vigenère yn defnyddio seiffr Caesar gyda sifft wahanol ym mhob safle'r testun; diffinnir gwerth y shifft gan ddefnyddio allweddair sy'n ailadrodd. Os yw'r allweddair cyhyd â'r neges, yn cael ei ddewis ar hap, byth yn dod yn hysbys i unrhyw un arall, ac nad yw byth yn cael ei hailddefnyddio, yna profwyd na ellir byth ei dorri. Mae'r amodau hyn mor anodd, i bob pwrpas maent byth yn cael eu cyflawni. Mae allweddeiriau sy'n fyrrach na'r neges (e.e., roedd y Cydffederaliaeth ystod Rhyfel Cartref America yn defnyddio seiffr Vigenère gyda'r allweddair "Complete Victory"), yn cyflwyno patrwm cylchol. Yn yr achosion hyn gellir ei ganfod gyda fersiwn fwy cymhleth o ddadansoddiad amledd.[10]

Ym mis Ebrill 2006, cipiwyd pennaeth y Maffia, Bernardo Provenzano, yn Sisili, rhannol oherwydd cafodd rhai o'i negeseuon, a ysgrifennwyd gan ddefnyddio amrywiad o'r seiffr Caesar, eu torri. Defnyddiodd Provenzano seiffr gyda rhifau, byddai "A" yn cael ei ysgrifennu fel "4", "B" fel "5", ac ati.[11]

Yn 2011, cafwyd Rajib Karim yn euog yn y Deyrnas Unedig o "droseddau terfysgaeth" ar ôl defnyddio'r seiffr Caesar i gyfathrebu ag actifyddion Islamaidd o Fangladesh i drafod cynlluniau i ffrwydro awyrennau British Airways neu darfu ar eu rhwydweithiau TG. Er bod gan y partïon fynediad at dechnegau amgryptio llawer gwell, fe wnaethant ddewis defnyddio eu cynllun eu hunain, a weithredwyd yn Microsoft Excel.[12]

Torri'r cipher[golygu | golygu cod]

Sifft i'w datgryptio Testun-blaen ymgais
0 >exxegoexsrgi 
1 dwwdfndwrqfh 
2 cvvcemcvqpeg 
3 buubdlbupodf
4 attackatonce 
5 zsszbjzsnmbd 
6  yrryaiyrmlac
. . .
23  haahjrhavujl
24  gzzgiqgzutik
25 fyyfhpfytshj 

Gellir torri seiffr Caesar yn hawdd hyd yn oed mewn os oes gennych y destun-seiffr yn unig. Gellir ystyried dwy sefyllfa:

  1. mae ymosodwr yn gwybod (neu'n dyfalu) bod rhyw fath o seiffr amnewid syml wedi'i ddefnyddio, ond nid yn benodol ei fod yn gynllun Caesar;
  2. mae ymosodwr yn gwybod bod seiffr Caesar yn cael ei ddefnyddio, ond nid yw'n gwybod gwerth y sifft.

Yn yr achos cyntaf, gellir torri'r seiffr gan ddefnyddio'r un technegau ag ar gyfer seiffrau amnewid syml cyffredinol, er enghraifft dadansoddi amledd.[13] Wrth wneud hwn, mae'n debygol y bydd ymosodwr yn sylwi'n gyflym bod yna batrwm rheolaidd ac felly'n diddwytho mai seiffr Caesar a ddefnyddir.

Mae gan ddosraniad llythrennau mewn sampl nodweddiadol o destun Saesneg siâp unigryw a rhagweladwy. Mae seiffr Caesar yn sifftio'r y dosbarthiad hwn, ac mae'n bosibl darganfod y sifft benodol a defnyddir trwy edrych ar y graff amledd.

Yn yr ail achos, mae torri'r cynllun hyd yn oed yn fwy syml. Gan mai dim ond nifer gyfyngedig o sifftiau posib (29 yn Gymraeg, 25 yn Saesneg), gellir ceisio pob un yn ei dro mewn ymosodiad "brute-force".[14] Un ffordd o wneud hyn yw ysgrifennu darn bach o'r destun-seiffr mewn tabl o'r holl sifftiau posib.[15][16] Rhoddir enghraifft ar gyfer y destun-seiffr Saesneg "EXXEGOEXSRGI"; gallwn adnabod y destun-plaen ar unwaith fel sifft o bedwar.

Dull "brute-force" arall yw ceisio cyfateb dosraniadau amledd y llythrennau. Trwy graffio amleddau llythrennau yn y destun-seiffr, a thrwy wybod dosraniad disgwyliedig y llythrennau hynny yn iaith wreiddiol y destun-plaen, gallwn yn weddol hawdd sylwi ar werth y sifft trwy edrych ar ddadleoliad nodweddion penodol y graff. Gelwir hyn yn ddadansoddiad amledd. Er enghraifft, yn yr iaith Saesneg amleddau'r llythrennau E, T, yw'r amlaf, ac Q, Z yw'r lleiaf aml.[17] Gall cyfrifiaduron hefyd wneud hyn trwy fesur pa mor dda y mae'r dosraniad amledd gwirioneddol yn cyd-fynd â'r dosbarthiad disgwyliedig; er enghraifft gan ddefnyddio'r ystadegyn -sgwâr.[18]

Gyda'r seiffr Caesar, nid yw amgryptio testun sawl gwaith yn darparu unrhyw ddiogelwch ychwanegol. Y rheswm am hyn yw y bydd dau amgryptiad o, dyweder, sifft A a sifft B, yn cyfateb i amgryptiad sengl gyda sifft A + B. Yn nhermau mathemategol, mae'r set o weithrediadau amgryptio o dan bob allwedd bosibl yn ffurfio grŵp o dan gyfansoddiad.[19]

Cyfeiriadau[golygu | golygu cod]

  1. ↑ Suetonius, Vita Divi Julii 56.6
  2. ↑ Luciano, Dennis; Gordon Prichett (January 1987). "Cryptology: From Caesar Ciphers to Public-Key Cryptosystems". The College Mathematics Journal 18 (1): 2–17. doi:10.2307/2686311. JSTOR 2686311. https://archive.org/details/sim_college-mathematics-journal_1987-01_18_1/page/2.
  3. ↑ Wobst, Reinhard (2001). Cryptology Unlocked. Wiley. t. 19. ISBN 978-0-470-06064-3.
  4. ↑ "Cracking the Code". Central Intelligence Agency. Archifwyd o'r gwreiddiol ar 2020-12-26. Cyrchwyd 21 February 2017.
  5. ↑ Singh, Simon (2000). The Code Book. Anchor. tt. 289-290. ISBN 0-385-49532-3.
  6. ↑ Pieprzyk, Josef; Thomas Hardjono; Jennifer Seberry (2003). Fundamentals of Computer Security. Springer. t. 6. ISBN 3-540-43101-2.
  7. ↑ Singh, Simon (2000). The Code Book. Anchor. tt. 14–20. ISBN 0-385-49532-3.
  8. ↑ Kahn, David (1967). The Codebreakers. tt. 775–6. ISBN 978-0-684-83130-5.
  9. ↑ Kahn, David (1967). The Codebreakers. tt. 631–2. ISBN 978-0-684-83130-5.
  10. ↑ Kahn, David (1967). The Codebreakers. ISBN 978-0-684-83130-5.
  11. ↑ Leyden, John (2006-04-19). "Mafia boss undone by clumsy crypto". The Register. Cyrchwyd 2008-06-13.
  12. ↑ "BA jihadist relied on Jesus-era encryption". The Register. 2011-03-22. Cyrchwyd 2011-04-01.
  13. ↑ Beutelspacher, Albrecht (1994). Cryptology. Mathematical Association of America. tt. 9–11. ISBN 0-88385-504-6.
  14. ↑ Beutelspacher, Albrecht (1994). Cryptology. Mathematical Association of America. tt. 8–9. ISBN 0-88385-504-6.
  15. ↑ Leighton, Albert C. (April 1969). "Secret Communication among the Greeks and Romans". Technology and Culture 10 (2): 139–154. doi:10.2307/3101474. JSTOR 3101474. https://archive.org/details/sim_technology-and-culture_1969-04_10_2/page/139.
  16. ↑ Sinkov, Abraham; Paul L. Irwin (1966). Elementary Cryptanalysis: A Mathematical Approach. Mathematical Association of America. tt. 13–15. ISBN 0-88385-622-0.
  17. ↑ Singh, Simon (2000). The Code Book. Anchor. tt. 72–77. ISBN 0-385-49532-3.
  18. ↑ Savarese, Chris; Brian Hart (2002-07-15). "The Caesar Cipher". Archifwyd o'r gwreiddiol ar 2020-05-24. Cyrchwyd 2008-07-16.
  19. ↑ Wobst, Reinhard (2001). Cryptology Unlocked. Wiley. t. 31. ISBN 978-0-470-06064-3.
Wedi dod o "https://cy.wikipedia.org/w/index.php?title=Seiffr_Caesar&oldid=11844812"