Rhif anghymarebol
Mewn mathemateg, mae'r rhifau anghymarebol (Irrational number) yn cynnwys yr holl rifau real nad ydynt yn rifau cymarebol. Rhif anghymarebol, felly, yw gwrthwyneb rhif cymarebol. Rhif cymarebol yw'r rhifau a grëwyd o gymarebau (neu ffracsiynau) o gyfanrifau (integers). Pan fo'r gymhareb o hyd segment dwy linell yn rhif anghymarebol, disgrifir segmentau'r linell fel rhywbeth anghymesur, gan olygu nad oes dim yn gyffredin rhyngddynt o ran 'mesur'; nid oes hyd ("y mesur") y gellid ei ddefnyddio i fynegi hyd y ddau segment a roddwyd fel lluosrifau cyfanrif (integer multiples) ohono'i hun.
Ymhlith y rhifau anghymarebol mae:
- cymhareb π o gylchedd cylch at ei diamedr,
- rhif Euler,
- y gymhareb aur φ
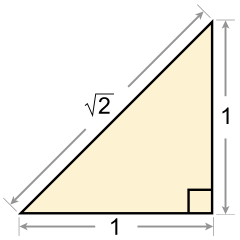
- ail isradd 2
- pob ail isradd o rifau naturiol, ar wahân i sgwariau perffaith.[1][2][3]
Gellir dangos nad yw rhifau anghymarebol, pan fynegir eu bod mewn system rifol e.e. fel rhif degol, neu fathau naturiol eraill, yn dod i ben, nac yn ailadrodd, hy, ddim yn cynnwys dilyniant o ddigidau. Er enghraifft, mae cynrychiolaeth degol y rhif π yn dechrau gyda 3.14159, ond ni all unrhyw nifer meidraidd o ddigidiau gynrychioli π yn union, ac nid yw'n ailadrodd.
O ganlyniad i brawf Cantor na ellir cyfrif y rhifau real a bod modd cyfri y rhifau cymarebol, mae'n dilyn bod bron pob un o'r niferoedd real yn anghymarebol.[4]
Cyfeiriadau[golygu | golygu cod]
- ↑ The 15 Most Famous Transcendental Numbers. by Clifford A. Pickover. URL retrieved 24 Hydref 2007.
- ↑ http://www.mathsisfun.com/irrational-numbers.html; URL retrieved 24 Hydref 2007.
- ↑ Weisstein, Eric W. "Irrational Number". MathWorld. URL retrieved 26 Hydref 2007.
- ↑ Cantor, Georg (1955) [1915]. Philip Jourdain (gol.). Contributions to the Founding of the Theory of Transfinite Numbers. New York: Dover. ISBN 978-0-486-60045-1.
